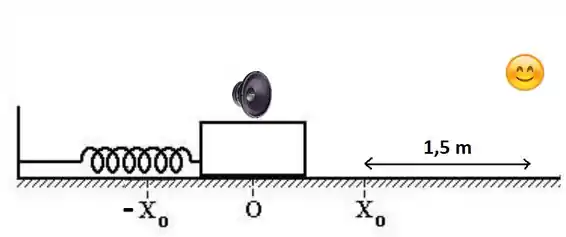
Um alto falante, mostrado na figura abaixo, que emite um sinal sonoro com frequência de 440 Hz, foi conectado a um sistema massa-mola. O sistema realiza um movimento harmônico simples com velocidade máxima de 6 m/s e amplitude de oscilação de 0,5 m. O alto falante se move para a direita e para a esquerda, se aproximando e se afastando de um ouvinte que se encontra em repouso.
A separação mínima entre o ouvinte e o alto falante é de 1,5 m. Considere o alto falante uma fonte pontual isotrópica.
a) Determine a maior e a menor frequência detectada pelo ouvinte.
Considere em seguida que o nível sonoro máximo detectado pelo ouvinte é de 60 dB, quando a fonte está mais próxima do ouvinte.
b) A intensidade do som na posição do ouvinte, em W/m2, quando o alto falante estiver mais próximo do ouvinte;
c) A potência do alto falante;
d) O nível sonoro, em dB, quando o alto falante estiver na posição mais afastada possível do ouvinte.
Passo 1
a) Bom, o que tá acontecendo aí é um cara chamado Efeito Dopler. No efeito Dopler, a frequência detectada pelo ouvinte é diferente da emitida pelo observador.
A gente usa essa fórmula:
Em que:
é a frequência detectada pelo observador;
é a frequência da fonte;
é a velocidade do observador;
é a velocidade da fonte;
é a velocidade do som no ar.
Já sabemos que é zero porque o observador está parado. Então:
Para máximo usaremos o sinal negativo, fonte se aproximando do observador:
E vemos que será máxima quando for máxima, ou seja, igual a 6 m/s.
Então:
Para mínimo usaremos o sinal positivo, fonte se distanciando do observador:
E será mínima também para máxima. Então:
Show!
Passo 2
b) Ele disse pra gente que o nível sonoro detectado pelo ouvinte quando a fonte está mais próxima é de 60 dB. Temos uma fórmula que relaciona o nível sonoro com a intensidade:
Em que W/m2.
Então, trocando:
Passo 3
c) Nós já temos a intensidade quando a fonte está mais próxima do ouvinte. Tem uma fórmula pra intensidade em função da potência:
Em que d é a distância entre o ouvinte e a fonte, no caso . Então:
Passo 4
d) Vamos calcular a intensidade sonora quando a fonte está mais distante do ouvinte:
O nível sonoro vai ser:
Resposta
a) e
b)
c)
d)