Uma onda transversal senoidal com um comprimento de onda de 80 cm propaga-se no sentido positivo de um eixo x. A figura abaixo mostra a velocidade transversal da partícula situada em x = 0 em função do tempo.
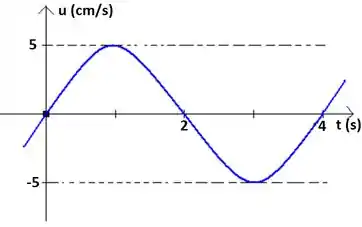
a) Determine a frequência e a velocidade de propagação da onda.
b) Determine a amplitude da onda (máximo deslocamento das partículas).
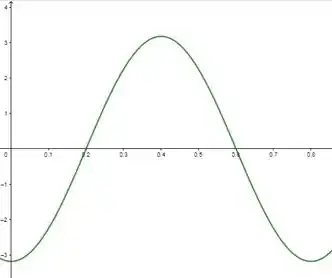
c) Determine a função de onda y(x,t) e faça o gráfico entre x = 0 e x = 80 cm no instante t = 2 s.
Considere agora que a onda acima se superponha a outra onda com a mesma frequência e mesma amplitude, mas com uma diferença de fase em relação a ela.
d) Encontre a diferença de fase para que a taxa média de energia transportada pela onda resultante seja o dobro da transportada por cada onda, separadamente.
Passo 1
a) Nós sabemos que a função de uma onda é parecida com isso aqui:
Repare que eu coloquei um sinal de menos ali no porque tá se propagando no sentido positivo do eixo x.
Se nós derivarmos essa função em relação a t encontramos a velocidade das partículas, que é o gráfico que ele deu. Então:
E fazendo x = 0:
Pelo gráfico, T = 4 s. E como:
Show! Temos uma relação pra frequência também:
Então:
Passo 2
Além disso tudo, como ele disse o comprimento de onda nós temos:
Passo 3
b) O gráfico dado é:
E a amplitude é igual a 0,05 m/s. Então:
Passo 4
Nós precisamos achar:
Já conhecemos e A, faltam e k.
Para achar vamos fazer:
Quando derivamos com relação ao tempo, achamos a velocidade transversal. E como o gráfico que ele deu foi de velocidade, vamos pegar o ponto do gráfico em que , porque nesse gráfico já é zero. Então:
Então:
Para achar k:
Como nós já temos o comprimento de onda que é 0,8 m:
Então:
Para t = 2 s:
E o gráfico vai ficar mais ou menos assim:
Passo 5
d) Esse item D é muito chato! Compartilho do seu sofrimento, tô contigo. Vamos com calma que vai dar certo, may the Force be with us.
Tem uma coisa que você precisa saber. A taxa média de energia transportada é a potência média. E a potência é proporcional ao quadrado da amplitude!
A potência da onda resultante vai ser então:
Esse sinalzinho quer dizer proporcional.
E a potência das ondas originais é:
Porque as ondas originais têm a mesma amplitude.
Como nós queremos que:
Então a relação entre as amplitudes deve ser:
Show? Grave isso!
Passo 6
A segunda onda vai ter uma equação assim:
Tem a mesma amplitude, a mesma frequência e a mesma velocidade (a velocidade só depende do meio) que a primeira, só muda a diferença de fase.
A onda resultante vai ser a soma das duas:
E substituindo:
Passo 7
Show! Agora, vem uma pegada de trigonometria. Vamos usar a fórmula:
Então:
Repare que a amplitude é a parte da função que não varia. A amplitude vai ser então:
Beleza! Mais um pouco de trigonometria. Vamos usar a fórmula:
Passo 8
Maravilha! Vamos lembrar da relação que a gente tinha achado antes:
Substituindo o valor de A:
Vamos elevar ao quadrado dos dois lados, ok?
Lembrando que:
E que:
Vamos trocar:
Então:
Ufa.
Resposta
a) ,
b)
c)
d)