Uma corda de violino de 30 cm de comprimento com uma massa específica linear de 0,65 g/m é colocada perto de um alto-falante alimentado por um oscilador de áudio de frequência variável. Observa-se que a corda entra em oscilação apenas nas frequências de 880 Hz e 1320 Hz, quando a frequência do oscilador de áudio varia no intervalo de 500 a 1500 Hz.
a) Determine a que harmônicos correspondem as frequências de 880 e 1320 Hz e faça um esboço da forma de oscilação da corda nesses dois modos.
b) Determine a tensão na corda.
Passo 1
a) Nós sabemos que o a frequência na corda em função do harmônico é:
A corda entra em oscilação nas frequências de 880 Hz e 1320 Hz. Aí que vem o pulo do gato! A frequência de 880 Hz vai corresponder a um harmônico, e a frequência de 1320 Hz ao harmônico seguinte.
Então podemos dizer:
Passo 2
Show! Vou isolar na primeira:
Substituindo na segunda:
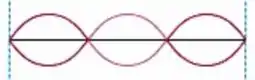
Achamos nessa continha então que as frequências de 880 Hz e 1320 Hz correspondem ao segundo e terceiro harmônico respectivamente.
E as formas de oscilação nesses dois modos:
:

:
Passo 3
b) Vamos voltar na frequência do segundo harmônico:
Maravilha! Temos uma fórmula que relaciona tensão na corda e velocidade:
Substituindo:
Resposta
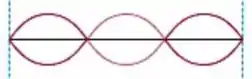
a) As frequências de 880 Hz e 1320 Hz correspondem ao segundo e terceiro harmônico respectivamente.
:

:
b)