P3 de Física 2- FIS1041 da PUCRIO - 2015.1

Uma jarra com litros de limonada ficou sobre uma mesa de piquenique durante todo o dia e atingiu a temperatura de . Você despeja dessa limonada ( em um copo de isopor, adiciona 2 cubos de gelo(cada um com a e tampa. Supondo que nenhum calor seja trocado com o ambiente, determine:

1. A temperatura final da limonada.
2. A temperatura final se você adicionar seis cubos de gelo, ao invés de só dois.

Dados:

Três mols de nitrogênio estão em uma caixa cúbica e rígida, com lados medindo Determine:

c) A força que o gás exerce sobre cada um dos seis lados da caixa quando a temperatura é de

d) O trabalho realizado pelo gás quando a sua temperatura aumenta pra

e) O número de graus de liberdade das moléculas e a energia cinética média por molécula no estado inicial.

f) A velocidade média quadrática no estado inicial.

Dados:

Uma amostra de gás Hélio está incialmente à pressão , volume ( 1 litro) e temperatura O gás é expandido isotermicamente até seu volume atingir . Em seguida, é comprimido à pressão constante até determinado volume e retorna ao seu estado inicial após uma compressão adiabática.

1. Faça um esquema desse ciclo em um diagrama (pressão x volume).
2. Encontre o valor de para o gás hélio e obtenha o valor de para essa amostra (coloque unidades).
3. Calcule o volume e a temperatura após a compressão isobárica.
4. Calcule o trabalho realizado no ciclo.
5. Calcule o rendimento da máquina que trabalha segundo esse ciclo.

Dados:

A figura mostra o diagrama pressão x volume do ciclo termodinâmico a que é submetido de um gás ideal poliatômico. As setas indicam o sentido do ciclo. Na figura , e

Para os itens (a), (b) e (c) assuma que a curva é isotérmica.

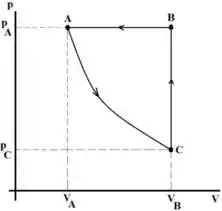
1. Calcule o valor de e .
2. Calcule o trabalho realizado pelo gás no ciclo.
3. Calcule a variação de entropia na trajetória .

Para os itens (d), (e) e (f) assuma que a curva é adiabática.

4. Calcule o valor de e .
5. Calcule o valor do trabalho feito no ciclo.
6. Calcule a variação de entropia na trajetória

Dados: