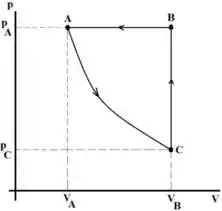
A figura mostra o diagrama pressão x volume do ciclo termodinâmico a que é submetido de um gás ideal poliatômico. As setas indicam o sentido do ciclo. Na figura , e

Para os itens (a), (b) e (c) assuma que a curva é isotérmica.

1. Calcule o valor de e .
2. Calcule o trabalho realizado pelo gás no ciclo.
3. Calcule a variação de entropia na trajetória .

Para os itens (d), (e) e (f) assuma que a curva é adiabática.

4. Calcule o valor de e .
5. Calcule o valor do trabalho feito no ciclo.
6. Calcule a variação de entropia na trajetória

Dados:

b):

O trabalho do ciclo é dado pelo trabalho dos trechos e

Por que não tem trabalho no trecho Por que ali não há variação de volume!

Então:

E o trabalho é o trabalho de uma transformação isotérmica, então:

Só que, como

E usando a equação geral dos gases:

Então:

Então o trabalho do ciclo é:

c):

Bom, a variação de entropia vai ser a soma das variações de entropia de cada etapa. Perceba que ele não quer a variação do ciclo inteiro, e sim só do trajeto

Vamos calcular cada um:

: É uma transformação isobárica. Bom, aqui a gente precisa lembrar da equação básica da entropia:

Show? No caso, como a transformação é isobárica, o vai ser:

Usamos , sacou?:

Como:

Então:

E vai acontecer numa variação isovolumétrica(por isso vamos usar

Como

Somando:

Agora, lembrando que e

d):

Bom, agora vamos supor que a acurva é uma adiabática. Show?

Bora então:

Pra achar , vamos usar a equação abaixo:

Lembrando que

Então:

E pra achar a temperatura a gente usa a velha e boa equação geral dos gases:

e):

Como em não há variação de volume, também não há trabalho ali. Então o trabalho total será dado por:

Show?

O trabalho de é simples já que é uma transformação isobárica:

Já o trabalho de a gente descobre usando a primeira lei da termo, lembrando-se que na transformação adiabática não há troca de calor:

Lembra da letra a)? Já a gente calculo no item anterior, então:

E então, somando geral:

f):

Como a gente vai calcular isso? Simples, vamos partir do fato de que em um ciclo, a variação total de entropia é nula.

Beleza, mas nós não queremos calcular a variação do ciclo....queremos apenas do trecho . Bom, mas se fecharmos o ciclo, isso é, incluir o outro trecho numa equação, vamos encontrar um resultado interessante:

Show?

Então se a gente calcular a variação a gente calcula a outra variação. Mas pera, esse trecho não é uma adiabática?

Lembra que, como não há transferência de calor nesses processos, não há variação de entropia?

Então:

Logo:

Pronto (: