Três mols de nitrogênio estão em uma caixa cúbica e rígida, com lados medindo Determine:

c) A força que o gás exerce sobre cada um dos seis lados da caixa quando a temperatura é de

d) O trabalho realizado pelo gás quando a sua temperatura aumenta pra

e) O número de graus de liberdade das moléculas e a energia cinética média por molécula no estado inicial.

f) A velocidade média quadrática no estado inicial.

Dados:

Agora, pra calcular a força que a essa pressão exerce em cada parede do recipiente, basta a gente usar a relação da fora com a pressão:

Bom, a área de uma parede é:

Então:

d)

O que é o trabalho realizado por um gás? Não é dado pela integral abaixo?

Mas se não houver variação de volume, só de temperatura, tem como haver trabalho?

Claro que não! Então:

Show?

e):

Bom, a molécula de Nitrogênio tem dois átomos, ou seja, é diatômica. Então, ela tem três graus de liberdade de translação e dois graus de liberdade de rotação.

Um total de 5 graus de liberdade:

Olhando a nossa tabelinha:

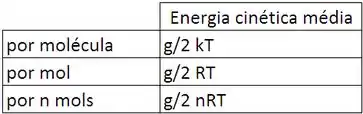
Vemos que a fórmula pra calcular a energia cinética por molécula é:

Onde é a constante de Boltzmann:

Assim:

Bem, vale:

Então:

f):

Como vamos resolver isso?

Bem, sabemos que a energia cinética de translação, do curso de mecânica, é dada por:

Então, a mesma energia pra uma molécula vaiser dada por:

Onde é a velocidade quadrática média que queremos achar.

Legal? Bom, mas nós queremos achar essa velocidade, e não sabemos com o que devemos comparar a equação da energia acima.

Mas lembra do item anterior? Bom, a energia cinética por molécula é dada por:

Só que queremos apenas a energia cinética de translação. Então o que faremos? Usaremos apenas os graus de liberdade de translação. Isso é:

Então:

Quanto é a massa de uma molécula? Basta a gente dividir o valor da massa molar pelo numero de moléculas que tem em um mol, ou seja, dividir pelo numero de Avogadro(

Então:

Assim: