Uma amostra de gás Hélio está incialmente à pressão , volume ( 1 litro) e temperatura O gás é expandido isotermicamente até seu volume atingir . Em seguida, é comprimido à pressão constante até determinado volume e retorna ao seu estado inicial após uma compressão adiabática.
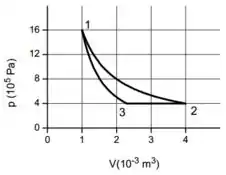
- Faça um esquema desse ciclo em um diagrama (pressão x volume).
- Encontre o valor de para o gás hélio e obtenha o valor de para essa amostra (coloque unidades).
- Calcule o volume e a temperatura após a compressão isobárica.
- Calcule o trabalho realizado no ciclo.
- Calcule o rendimento da máquina que trabalha segundo esse ciclo.
Dados:
Passo 1
a):
Essa é fácil. Basta que a gente lembre mais ou menos o formato de cada curva. O gráfico fica assim:
Passo 2
b):
O valor de já é tabelado pra gases monoatômicos e vale:
E pra calcular o valor de ,a gente pode usar a equação:
Podemos usar os valores do ponto 1:
Passo 3
c):
Pra gente descobrir o volume , é mais fácil usar o caminho da adiabática do que o da compressão isobárica.
Por que? Porque ai a gente usa a equação abaixo:
Show! Agora queremos saber a temperatura Pra isso usaremos a equação geral dos gases:
Passo 4
d):
Vamos calcular o trabalho de cada etapa e depois somar tudo:
O caminho é uma isoterma, então o trabalho é calculado por:
O caminho é um caminho isobárico, então o cálculo do trabalho é bem simples:
E o caminho é uma adiabática:
Pela primeira lei da termodinâmica, e por sabermos que numa transformação adiabática não há troca de calor, temos:
Show? Então, o trabalho é igual à variação da energia interna no processo.
Bom, essa variação pode ser calculada por:
Agora é só jogar o valor de que a gente achou:
Então:
Logo, o trabalho total é a soma de todos os trabalhos:
Passo 5
e):O rendimento é calculado por:
Onde é o calor fornecido pela fonte quente.
Ai vem uma dica: Pra você saber em qual trecho o gás recebe esse calor, basta você lembrar que é onde ele se expande, onde o seu volume aumenta.
No caso, no trecho : .
Só que como a temperatura não varia de pra 2, a variação de energia interna é nula. Isso gera, pela primeira lei da termodinâmica:
A gente já calculou o trabalho nesse trecho e esse vale:
Então:
Resposta
a):
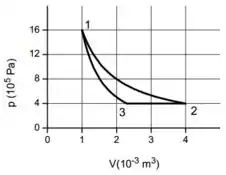
b):
c):
d):
e):