P4 de Física 2- FIS1041 da PUCRIO - 2014.1
Física 2- FIS1041 - PUCRIO
I-Uma onda estacionária transversal em uma corda longa possui um antinó em e um nó vizinho em A figura ao lado mostra o deslocamento da partícula da corda situada em .
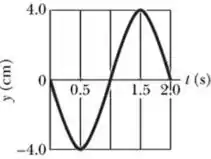
- Obtenha o comprimento de onda, o período e a máxima amplitude das oscilações na corda.
- Escreva a função representada no gráfico, especificando valores numéricos das constantes e suas unidades.
- Obtenha a função que representa a onda (vibração) estacionária (especificando valores numéricos das constantes e suas unidades).
- Faça o desenho da corda no instante no intervalo de a
- Obtenha a função que descreve a velocidade transversal das partículas da corda e calcule a velocidade da partícula situada em no instante
I- A figura abaixo mostra uma pequena esfera de ferro () suspensa por uma corda fina de massa desprezível presa em um cilindro que flutua parcialmente submerso, com as bases paralelas à superfície da água. O cilindro tem altura , área da base e massa específica . Um terço da altura do cilindro está acima da superfície da água.
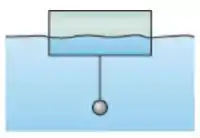
- Faça o diagrama de forças que atuam no sistema (esfera+cilindro) e obtenha o volume da esfera de ferro em função do volume do cilindro ().
II. A figura abaixo mostra um medidor Venturi, usado para medir a velocidade de um fluido num cano. Ele consiste de um segmento de cano de diâmetro com um estreitamento de diâmetro e um manômetro que mede a diferença de pressão entre a parte mais larga e mais estreita. Aplicando a equação da continuidade e a Equação de Bernoulli aos pontos 1 e 2,
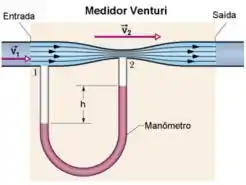
b) encontre a expressão da velocidade em função dos diâmetros , da massa específica do fluido e da diferença de pressão ().
c) Suponha que o fluido seja água doce, que o diâmetro do cano seja e o do estreitamento , e que a diferença de pressão seja . Calcule a vazão de água em e em ?
Ver solução completaO ciclo da figura abaixo representa a operação de um motor de combustão interna a gasolina. O volume . Suponha que a mistura de admissão gasolina-ar seja de um gás ideal () e com .
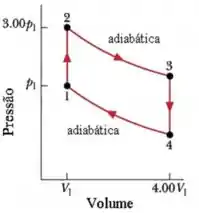
- Determine as razões
- Determine as razões,.
- Calcule a eficiência deste motor.
- Calcule a variação de entropia para os processos .