I-Uma onda estacionária transversal em uma corda longa possui um antinó em e um nó vizinho em A figura ao lado mostra o deslocamento da partícula da corda situada em .
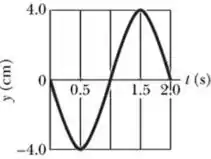
- Obtenha o comprimento de onda, o período e a máxima amplitude das oscilações na corda.
- Escreva a função representada no gráfico, especificando valores numéricos das constantes e suas unidades.
- Obtenha a função que representa a onda (vibração) estacionária (especificando valores numéricos das constantes e suas unidades).
- Faça o desenho da corda no instante no intervalo de a
- Obtenha a função que descreve a velocidade transversal das partículas da corda e calcule a velocidade da partícula situada em no instante
Passo 1
a): A máxima amplitude de oscilação e o período podem ser vistos a partir do gráfico. Como o gráfico mostra um perfil completo de uma onda, o valor de vai ser o último valor de tempo que aparece:
O valor máximo de amplitude é o maior valor de :
Já o valor de pode ser obtido se percebemos que:
Ou seja, o comprimento é quatro vez a distância de um nó e seu antinó. Então:
Passo 2
b):
O modelo padrão pra uma onda é:
Como
Porém, o gráfico é como um gráfico do seno de um ângulo, só que invertido. Então:
Como:
E:
Então:
Passo 3
c):
Como a função apresenta um máximo em , ou seja, um antinó, a função que tem o tem que ser um cosseno já que:
Então, como a fórmula tem que ter seno, como vimos no item anterior:
Sendo:
E:
E:
Passo 4
d):
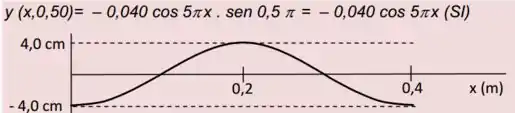
Passo 5
e):
Pra calcular a velocidade, basta a gente derivar a função do item c) em relação ao tempo:
Para:
Como:
Então:
Resposta
a):
b):
c):
d):
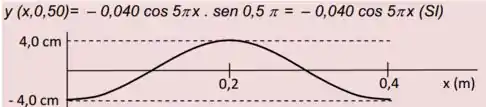
e):