O ciclo da figura abaixo representa a operação de um motor de combustão interna a gasolina. O volume . Suponha que a mistura de admissão gasolina-ar seja de um gás ideal () e com .
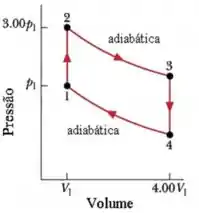
- Determine as razões
- Determine as razões,.
- Calcule a eficiência deste motor.
- Calcule a variação de entropia para os processos .
Passo 1
a):
Vamos lá:
Pra achar a relação entre e , basta a gente usar o Piviti-Povóto:
A relação entre e
Primeiro a gente usa a transformação adiabática que acontece entre 2 e 3:
Só que, usando o Piviti-Povóto:
Como já sabemos :
Relação entre e :
Basta a gente fazer a transformação adiabática entre e 1:
Usando Piviti-Povóto:
Substituindo o valor anterior:
Passo 2
b):
Bom, a gente já isolou essas frações no item anterior, certo?
Passo 3
c):
Bom galera, nós vamos usar:
Mas onde o calor é fornecido, isso é, onde o calor entra?
Bom, temos dois processos adiabáticos e dois isovolumétricos.
Sabemos que não é possível haver troca de calor nos processos adiabáticos, então nos resta os processos isovolumétricos.
Bem, um deles há aumento de pressão, , e no outro há uma diminuição de pressão, .
Onde o calor é fornecido? No !
Afinal de contas, com o fornecimento de energia, calor, as moléculas ganham energia e velocidade, o que faz aumentar a pressão, e não diminuir.
Então:
Como:
Então:
Vamos descobrir o valor de :
Então:
Beleza! Agora só precisamos descobrir o trabalho total do ciclo.
Passo 4
Como não há variação de volume nas duas transformações isovolumétricas, não há trabalho ali.
Só há trabalho sendo realizado nas duas transformações adiabáticas, certo?
E, além disso, pela primeira lei da termo:
E como numa transformação adiabática:
Então:
Como a variação de energia interna pode ser calculada por:
Mas como:
Então:
E:
Então, o trabalho total vai ser dado por:
Então, o rendimento será dado por:
Passo 5
d):
Como no processo não há transferência de calor, a variação de entropia é nula ali:
E no processo :
Com:
Então:
Como:
Então:
Lembrando que o valor de
Resposta
a):
b):
c):
d):