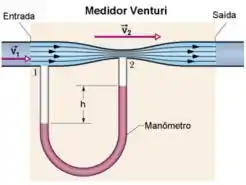
II. A figura abaixo mostra um medidor Venturi, usado para medir a velocidade de um fluido num cano. Ele consiste de um segmento de cano de diâmetro com um estreitamento de diâmetro e um manômetro que mede a diferença de pressão entre a parte mais larga e mais estreita. Aplicando a equação da continuidade e a Equação de Bernoulli aos pontos 1 e 2,
b) encontre a expressão da velocidade em função dos diâmetros , da massa específica do fluido e da diferença de pressão ().
c) Suponha que o fluido seja água doce, que o diâmetro do cano seja e o do estreitamento , e que a diferença de pressão seja . Calcule a vazão de água em e em ?
Passo 1
b):
Vamos aplicar a equação de Bernoulli nos dois pontos:
Como eles estão quase na mesma altura:
Isso quer dizer que as contribuições das alturas não importam e podemos escrever:
Passo 2
Mas queremos descobrir . Então temos que escrever em função de . Pra isso, vamos usar o principio da continuidade:
Com:
Então:
Logo:
Passo 3
c):
É só a gente aplicar os valores na formula que montamos antes pra achar , e depois multiplicarmos esse valor pelo valor da área
Assim:
Já que .
Resposta
a):
b):