1º EE de Física 2 da UFPE - 2019.2

A extremidade de uma viga homogênea, de peso P, está presa por uma dobradiça a uma parede vertical, como ilustra a figura. A outra extremidade da viga é sustentada por um fio inextensível e de massa desprezível, que faz o mesmo ângulo com a viga e com a parede. Considere que a aceleração da gravidade no local é constante, com a direção paralela à parede e sentido para baixo, como indicados pela pequena seta representada na figura.

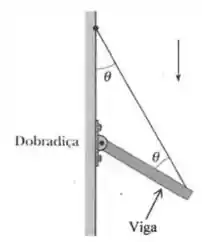
1. Esboce o diagrama do corpo livre da viga. Indique as direções e os pontos de aplicação das forças.

Nos itens abaixo, calcule em termos de P.

2. A tração no fio.
3. A componente vertical da força que a dobradiça exerce na viga. Indique se é para cima ou para baixo.
4. A componente horizontal da força que a dobradiça exerce na viga. Indique se é para a direita ou esquerda.

A figura ao lado mostra três esferas de massas localizadas nos vértices de um triângulo equilátero de lado . Uma quarta esfera de massa está localizada no centro do triângulo. Sabe-se que todas as esferas se mantêm fixas em suas posições. A constante de gravitação universal é dada por . Quando possível, expresse suas respostas em termos de , , e .

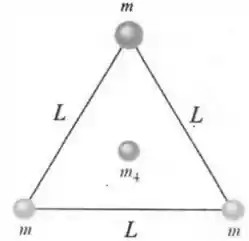
1. Considerando que a energia potencial gravitacional é nula no infinito, calcule a energia potencial entre a esfera de massa localizada no vértice superior do triângulo e a massa central .
2. Calcule o valor da força gravitacional resultante que as duas esferas de massa localizadas nos vértices inferiores do triângulo exercem sobre a esfera central de massa
3. Determine o valor da força gravitacional resultante total a que a massa central estará submetida por sua interação com todas as três massas . Justifique sua resposta.

A figura ao lado ilustra um recipiente cilíndrico (cilindro reto, de base circular) de área transversal , contendo líquido ideal de densidade . O cilindro é aberto para a atmosfera (pressão atmosférica ) na sua parte superior. A uma distância abaixo da superfície do líquido existe uma torneira cilíndrica de área transversal , por onde o fluido pode escoar com velocidade . Por outro lado, a velocidade da superfície do fluido é denotava por . Considere que a aceleração da gravidade no local é constante e representada por , como indicado na figura.

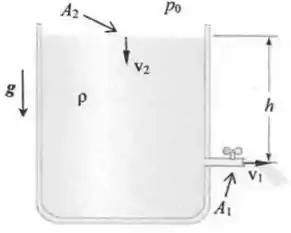
1. Usando a equação da continuidade, escreva em termos de , e .
2. Usando a equação de Bernoulli, calcule o valor de . Expresse seu resultado em termos de , , e .
3. Suponha que a tampa seja colocada na parte superior do cilindro e que o ar entre a tampa e o líquido seja mantido a pressão constante. Para esta situação, calcule o ovo valor de . Na sua resposta deste item considere que , de tal forma que . Expresse seu resultado em termos de , , , e .