A figura ao lado mostra três esferas de massas localizadas nos vértices de um triângulo equilátero de lado . Uma quarta esfera de massa está localizada no centro do triângulo. Sabe-se que todas as esferas se mantêm fixas em suas posições. A constante de gravitação universal é dada por . Quando possível, expresse suas respostas em termos de , , e .
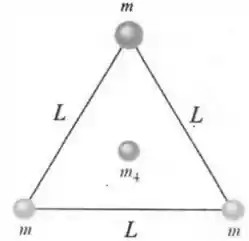
- Considerando que a energia potencial gravitacional é nula no infinito, calcule a energia potencial entre a esfera de massa localizada no vértice superior do triângulo e a massa central .
- Calcule o valor da força gravitacional resultante que as duas esferas de massa localizadas nos vértices inferiores do triângulo exercem sobre a esfera central de massa
- Determine o valor da força gravitacional resultante total a que a massa central estará submetida por sua interação com todas as três massas . Justifique sua resposta.
Passo 1
Vamos lá! Podemos começar escrevendo que a energia potencial entre duas partículas, considerando que no infinito a energia é zero, é dada por
Como as massas foram dadas, nosso problema se torna calcular a distância entre as duas partículas.
Se liga na figura.
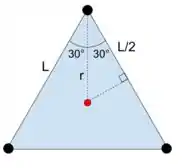
Como o nosso é a hipotenusa do nosso triangulo pequeno, podemos escrever que
Agora só precisamos substituir os valores na nossa expressão da energia potencial. Daí temos que
Pronto, acabamos o item (a).
Passo 2
No item (b), ele quer a força resultante que as duas esferas de massa localizadas nos vértices inferiores exercem sobre a massa .
A força gravitacional entre duas partículas de massa e é dada por
Para melhorarmos a nossa compreensão, podemos fazer um novo desenho indicando as forças.
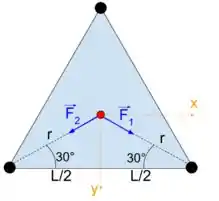
A distância entre as esferas da parte de baixo e a esfera do meio é a mesma que usamos no item (a).
Substituindo os valores, podemos escrever que
Passo 3
Como a força é um vetor, podemos observar na direção e o sentido das forças.
Como os ângulos da direção das forças em relação ao semieixo inferior são iguais, podemos observar que a componente do vetor puxa para a direita na mesma intensidade que a componente do vetor onde este puxa para a esquerda. Sendo assim, as componentes se anulam.
Ainda observando a simetria, podemos dizer que a magnitude das componentes em possuem a mesma magnitude, estão na mesma direção e sentido. Portanto, podemos calcular apenas uma e multiplicar por 2. Sendo assim
Multiplicando esta força por 2, temos
Passo 4
Como temos um triângulo equilátero com as esferas localizadas em seus vértices, ao colocarmos a massa no centro do triangulo, as forças que as esferas situadas nos vértices fazem sobre a esfera de massa terão a mesma intensidade e a resultante será nula, devido a simetria do sistema.
Observe do item (b), que as forças em se cancelaram. Quando calculamos a força de todas as massas, a resultante que achamos no item (b), se anulará com a força exercida pela esfera superior. Portanto a força resultante é nula.