3º EE de Física 2 da UFPE - 2019.2

Duas berras retilíneas idênticas, bastante finas, de comprimentos são unidas por suas extremidades, formando um angulo de entre si (veja figura ao lado). Ambas as barras tem coeficientes de dilatação linear dados por .

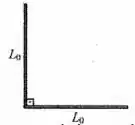
(a) (1,5) Se as barras são submetidas a uma variação de temperatura , calcule a soma dos comprimentos das barras após este processo. Expresse seu resultado em termos de , e .

(b) (2,0) Calcule a variação de temperatura a que deve ser submetida uma terceira barra, também de comprimento e de coeficiente de dilatação linear para que as duas barras resultantes do processo descrito no item (a) e esta terceira barra formem um triangulo retângulo. Expresse seu resultado em termos de e .

Suponha que moles de um gás ideal diatômico sofre um processo termodinâmico de um estado inicial de pressão , volume e temperatura para um estado final de pressão , volume e temperatura . Ao longo deste processo termodinâmico, a pressão varia proporcionalmente ao volume. Além disso, a velocidade média quadrática das moléculas dobra de valor entre os estudos inicial e final. Nestas condições, calcule.

1. (0,5) A temperatura final , expressando seu resultado em termos de . Dado: A energia cinética de translação média das moléculas de um gás ideal e , onde é a constante de Boltzmann.
2. (i) A pressão final , expressando seu resultado em termos de e (ii) o volume final expressando seu resultado em termos de .
3. O trabalho realizado pelo gás entre os estados inicial e final. Expresse seu resultado em termos de e .
4. O calor requerido para levar o sistema do estado inicial ao final. Expresse seu resultado em termos de e . Dado: Um gás ideal diatômico tem calor específico molar , onde é a constante universal dos gases.

A figura ao lado representa o diagrama pressão-volume de um ciclo termodinâmico que envolve um mol de um gás ideal que tem , onde é a constante universal dos gases.

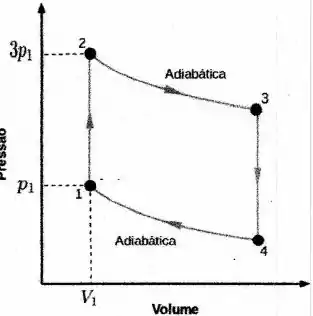
1. Calcule as temperaturas nos pontos e e em seguida o calor trocado pelo sistema no processo . Escreva suas respostas em termos de , e e em em termos de e .
2. Calcule a variação da entropia para os processos , , e de .
3. Sabendo que a eficiência da máquina térmica associada a tal ciclo é , calcule o trabalho por ciclo que ela realiza. Expresse sua resposta em termos de e .