A figura ao lado ilustra um recipiente cilíndrico (cilindro reto, de base circular) de área transversal , contendo líquido ideal de densidade . O cilindro é aberto para a atmosfera (pressão atmosférica ) na sua parte superior. A uma distância abaixo da superfície do líquido existe uma torneira cilíndrica de área transversal , por onde o fluido pode escoar com velocidade . Por outro lado, a velocidade da superfície do fluido é denotava por . Considere que a aceleração da gravidade no local é constante e representada por , como indicado na figura.
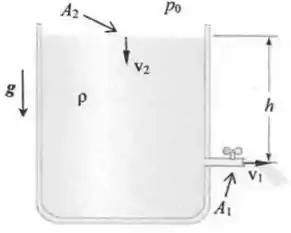
- Usando a equação da continuidade, escreva em termos de , e .
- Usando a equação de Bernoulli, calcule o valor de . Expresse seu resultado em termos de , , e .
- Suponha que a tampa seja colocada na parte superior do cilindro e que o ar entre a tampa e o líquido seja mantido a pressão constante. Para esta situação, calcule o ovo valor de . Na sua resposta deste item considere que , de tal forma que . Expresse seu resultado em termos de , , , e .
Passo 1
Vamos lá! Como no item (a) ele pede para usar a equação da continuidade, ou seja,
Ele pede para escrevermos . Portanto
Já acabamos o item (a). Vamos para o próximo.
Passo 2
No item (b), ele quer usando a equação de Bernoulli.
A equação de Bernoulli pode ser escrita como
Podemos ajustar essa equação como
Como queremos achar , precisamos isolar ele
Veja a figura.
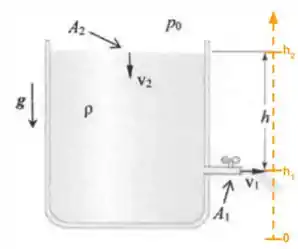
Repare que a
portanto
Passo 3
Como ele quer que a resposta esteja expressa em termos de , , e . Precisamos retomar o valor obtido no item (a). Lembrar que
Logo
Agora só precisamos manipular essa expressão, isolando .
Pronto. Resolvemos o item (b).
Passo 4
No item (c), precisamos levar em consideração que quando fechamos o cilindro, a pressão na borda de passa a ser constante . Então agora precisamos aplicar novamente a equação de Bernoulli
Levando em consideração que no enunciado diz para considerarmos que , temos
Então agora precisamos isolar o
Novamente usaremos que
Portanto
Pronto, finalizamos a questão.