A extremidade de uma viga homogênea, de peso P, está presa por uma dobradiça a uma parede vertical, como ilustra a figura. A outra extremidade da viga é sustentada por um fio inextensível e de massa desprezível, que faz o mesmo ângulo com a viga e com a parede. Considere que a aceleração da gravidade no local é constante, com a direção paralela à parede e sentido para baixo, como indicados pela pequena seta representada na figura.
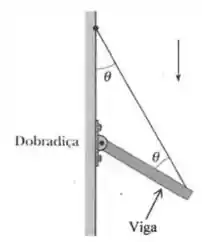
- Esboce o diagrama do corpo livre da viga. Indique as direções e os pontos de aplicação das forças.
- A tração no fio.
- A componente vertical da força que a dobradiça exerce na viga. Indique se é para cima ou para baixo.
- A componente horizontal da força que a dobradiça exerce na viga. Indique se é para a direita ou esquerda.
Nos itens abaixo, calcule em termos de P.
Passo 1
Vamos lá! Precisamos fazer o diagrama do corpo livre, ou seja, representar as forças, onde cada uma delas é aplicada, suas direções e sentidos.
Pela configuração descrita na figura, podemos desenhar o diagrama a seguir.
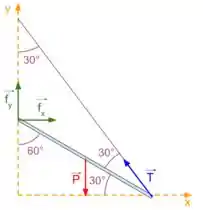
Onde representa o peso da viga e deve estar situado no centro de massa da barra, é a tração da corda e está orientada na direção do ponto de encontra da corda com a parede, e são as forças que a dobradiça faz nas direções horizontais e verticais, respectivamente.
Passo 2
No item (b), precisamos calcular a tração no fio. Para isso, devemos prestar atenção que quando um sistema mecânico está em equilíbrio temos que a força resultante é igual a zero e o torque resultante também.
Beleza?!
Por convenção, vamos usar que quando a força tende a fazer a viga no sentido horário, o torque será negativo. Quando tender a girar no anti-horário, será positivo.
Sendo o comprimento da viga e o ponto onde a dobradiça está, o ponto de rotação temos.
Lembre-se que forças aplicadas no ponto de rotação não causam torque.
Aplicando o valor das funções trigonométricas, temos
Matamos o item (b).
Passo 3
No item (c) ele pede a força vertical que a dobradiça exerce na viga. Para isso usaremos que a força resultante vertical sobre a barra deve ser zero.
Substituindo o valor da tração que achamos, podemos escrever que
Como podemos ver no diagrama, aponta para cima.
Passo 4
No item (d) ele pede a força horizontal que a dobradiça exerce na viga. Para isso usaremos que a força resultante na horizontal deve ser zero
Como podemos ver no diagrama, para que haja equilíbrio esta força deve estar orientada da esquerda para a direita.