2º EE de Física 2 da UFPE - 2019.2

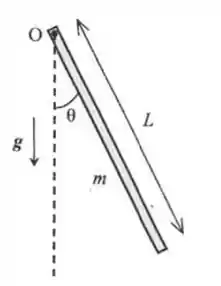
O pêndulo físico ilustrado na figura ao lado é composto por uma barra retilínea e homogênea, de comprimento e massa . Tal pêndulo oscila sob ação da gravidade em torno da sua posição de equilíbrio (linha tracejada vertical), tendo como ponto de suspensão o ponto , localizado no extremo superior da barra. Considere que a aceleração da gravidade no local é constante e representada por , como ilustrada na figura. Despreze quaisquer efeitos de atrito e resistência do ar. Nestas circunstâncias:

(a) Calcule o momento de inércia I deste pêndulo físico com relação ao ponto de suspensão . Dado: o momento de inércia da barra com relação a um eixo perpendicular à barra (ou seja, ao plano da página) e passando pelo seu centro de massa é

(b) Calcule o torque da força peso em relação ao ponto de suspensăo para o caso em que a barra faz um ângulo com a vertical. Expresse seu resultado para em termos de , e.

(c) Considere a aproximação de pequenas oscilações (onde ) e use a segunda lei de Newton para rotações para mostrar que o ângulo satisfaz uma equação do tipo oscilador harmônico. Em seguida, use tal equação para calcular o período das pequenas oscilações deste pêndulo fisico. Expresse seu resultado para em termos de e .

Considere um tubo de comprimento L fechado na sua extremidade esquerda e aberto para a atmosfera na sua extremidade direita, contendo ar em seu interior. Considere que a velocidade do som no ar seja dada por .

(a) Faça um desenho do tubo e represente os perfis das ondas geradas no seu interior, indicando as posições dos nós () e dos antinós () para os dois modos de frequência mais baixa das vibrações.

(b) Determine as frequências e dos dois modos mencionados na letra (a), escrevendo seus resultados em termos de e .

(c) Admitindo que e supondo que seja a frequência mais baixa que o ar no tubo entra em ressonância com o som emitido por um alto-falante próximo, determine o valor de .

Uma corda de massa especifica linear (ou, densidade linear de massa) é tensionada por uma força de tração. Ondas transversais são excitadas na corda e se propagam de acordo com a função senoidal

onde e são dados em metros e em segundos. Nestas condições, determine:

(a) O deslocamento transversal da corda quando e .

(b) O comprimento de onda

(c) O período .

(d) A velocidade de propagação da onda .

(e) A intensidade da força de tensão na corda.

(f) Se dobrarmos o valor da amplitude da onda dada pela função acima, de quanto aumenta a potência transmitida pela onda?