UFPE- Física geral 2 – P2 2019.2
Considere um tubo de comprimento L fechado na sua extremidade esquerda e aberto para a atmosfera na sua extremidade direita, contendo ar em seu interior. Considere que a velocidade do som no ar seja dada por .
(a) Faça um desenho do tubo e represente os perfis das ondas geradas no seu interior, indicando as posições dos nós () e dos antinós () para os dois modos de frequência mais baixa das vibrações.
(b) Determine as frequências e dos dois modos mencionados na letra (a), escrevendo seus resultados em termos de e .
(c) Admitindo que e supondo que seja a frequência mais baixa que o ar no tubo entra em ressonância com o som emitido por um alto-falante próximo, determine o valor de .
Passo 1
a)
Bom, temos um tubo fechado em um dos lados. Nesse caso, as frequências permitidas são
Com Então os dois modos de frequências mais baixas são quando e .
Show! Vamos desenhar agora o perfil das ondas e marcar os nós e antinós.
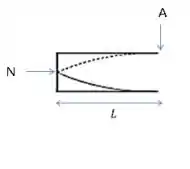
Para , temos , mas , então . Ou seja, teremos somente do comprimento de onda no tubo de comprimento .
Para , temos , mas , então . Ou seja, teremos do comprimento de onda no tubo de comprimento .
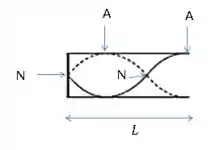
Show!
Passo 2
b)
Opa! Já até fizemos no ítem anterior!
Que lindo!!
Passo 3
c)
A frequência mais baixa é:
Então, agora é só substituir os valores:
Uhuul!
Resposta
a) imagens.
b)
c)