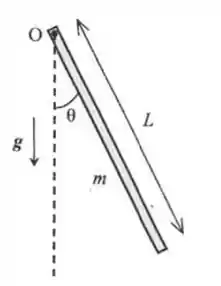
O pêndulo físico ilustrado na figura ao lado é composto por uma barra retilínea e homogênea, de comprimento e massa . Tal pêndulo oscila sob ação da gravidade em torno da sua posição de equilíbrio (linha tracejada vertical), tendo como ponto de suspensão o ponto , localizado no extremo superior da barra. Considere que a aceleração da gravidade no local é constante e representada por , como ilustrada na figura. Despreze quaisquer efeitos de atrito e resistência do ar. Nestas circunstâncias:
(a) Calcule o momento de inércia I deste pêndulo físico com relação ao ponto de suspensão . Dado: o momento de inércia da barra com relação a um eixo perpendicular à barra (ou seja, ao plano da página) e passando pelo seu centro de massa é
(b) Calcule o torque da força peso em relação ao ponto de suspensăo para o caso em que a barra faz um ângulo com a vertical. Expresse seu resultado para em termos de , e.
(c) Considere a aproximação de pequenas oscilações (onde ) e use a segunda lei de Newton para rotações para mostrar que o ângulo satisfaz uma equação do tipo oscilador harmônico. Em seguida, use tal equação para calcular o período das pequenas oscilações deste pêndulo fisico. Expresse seu resultado para em termos de e .
Passo 1
- Calcule o momento de inércia I deste pêndulo físico com relação ao ponto de suspensão . Dado: o momento de inércia da barra com relação a um eixo perpendicular à barra (ou seja, ao plano da página) e passando pelo seu centro de massa é
Aqui ele quer saber o momento de inércia do pêndulo em relação a um eixo que não é o eixo que passa pelo centro de massa.
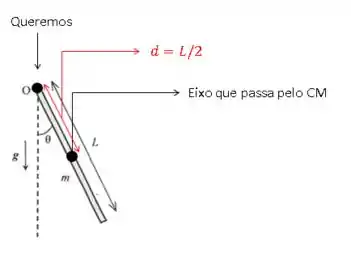
E aí, como resolvemos isso? Vamos usar o teorema dos eixos paralelos!
Onde esse é a distância entre o eixo novo e o centro de massa. No nosso caso, como a barra é homogênea, o centro de massa fica bem no meio, em . Então a distância do centro de massa a extremidade é
Agora é só substituir os dados:
Prontinho!!
Passo 2
(b) Calcule o torque da força peso em relação ao ponto de suspensăo para o caso em que a barra faz um ângulo com a vertical. Expresse seu resultado para em termos de , e.
Vamos fazer um diagrama de forças:
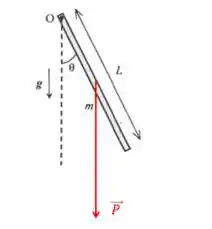
O torque da força peso em relação ao eixo é dado por:
O é o vetor que vai do eixo de rotação até o ponto de aplicação da força. Como a força peso é aplicada no centro de massa, temos que
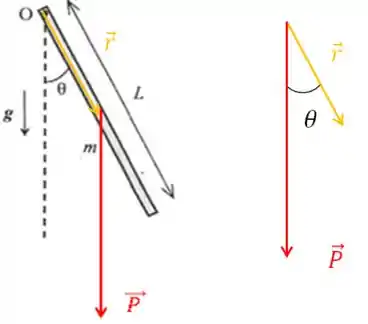
Note que a força peso faz o pêndulo girar no sentido horário, por convenção, esse é o sentido negativo. Isso também pode ser visto pela regra da mão direita. É só colocar a mão na direção e sentido do vetor e depois fechar a mão em direção ao vetor ,e então seu dedão aponta para dentro da página e o movimento que você fez com os dedos é no sentido horário.
Então o módulo do torque é:
E o sentido é horário.
Passo 3
c) Considere a aproximação de pequenas oscilações (onde ) e use a segunda lei de Newton para rotações para mostrar que o ângulo satisfaz uma equação do tipo oscilador harmônico. Em seguida, use tal equação para calcular o período das pequenas oscilações deste pêndulo físico. Expresse seu resultado para em termos de e .
A segunda lei de Newton para rotações é
Como já sabemos o e o , vamos substituir:
Arrumando u pouco:
Usando a aproximação de ângulos pequenos:
Beleza, mas lembra que é a aceleração angular, então
E essa é uma equação parecida com a equação do oscilador harmônico. Para ficar mais parecida ainda podemos escrever:
E aí:
Tá a cara do oscilador harmônico! rsrs
Aí agora ele pediu pra gente achar o período dessas oscilações. Então, a frequência angular, , é dada por:
Vimos que:
Então
Prontinho!!
Resposta
a)
b)
E o sentido é horário.
c)