Suponha que moles de um gás ideal diatômico sofre um processo termodinâmico de um estado inicial de pressão , volume e temperatura para um estado final de pressão , volume e temperatura . Ao longo deste processo termodinâmico, a pressão varia proporcionalmente ao volume. Além disso, a velocidade média quadrática das moléculas dobra de valor entre os estudos inicial e final. Nestas condições, calcule.
- (0,5) A temperatura final , expressando seu resultado em termos de . Dado: A energia cinética de translação média das moléculas de um gás ideal e , onde é a constante de Boltzmann.
- (i) A pressão final , expressando seu resultado em termos de e (ii) o volume final expressando seu resultado em termos de .
- O trabalho realizado pelo gás entre os estados inicial e final. Expresse seu resultado em termos de e .
- O calor requerido para levar o sistema do estado inicial ao final. Expresse seu resultado em termos de e . Dado: Um gás ideal diatômico tem calor específico molar , onde é a constante universal dos gases.
Passo 1
POW! O problema nos deu uma informação importantíssima. No finalzinho da letra A ele nos deu a informação de energia cinética:
E energia cinética de um gás também pode ser calculada por...
Então veja que estamos com a faca e o queijo para resolver esse item. Bora?
Passo 2
Igualando essas duas expressões acima...
Só que queremos a temperatura final em termos da inicial . Pela equação de cima a final a e a inicial, ambas tem que obedecer...
Sabemos do enunciado que a velocidade média quadrática dobra o valor no estágio final da transformação, isto é...
Elevando ao quadrado...
Como ou ...
Então...
Só que essa expressão em negrito é a temperatura inicial do gás...
Passo 3
Bem... Nesse item podemos usar o fato de que o Gás é ideal então é válida a expressão...
Só que do item A já descobrimos que , o que nos leva a...
O enunciado nos disse que a pressão varia proporcionalmente ao volume, isto é...
Então...
Passo 4
Para saber qual será o volume final em termos do inicial agora é de boa! Basta usar o fato de que...
Então...
Passo 5
POW! Queremos aqui então calcular a energia realizada pelo gás ao se expandir. Sabemos da Teoria que podemos encontrar essa energia (trabalho) calculando então a área sob o gráfico . Então vamos construir o gráfico dessa transformação beleza?
Bem... Para isso, sabemos da pressão inicial e do volume inicial . Sabemos também das pressões e volumes finais em relação às iniciais...
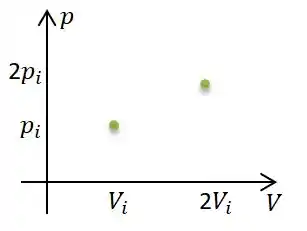
Além disso, sabemos que a pressão e o volume variam proporcionalmente entre si, isto significa que a transformação é uma reta...
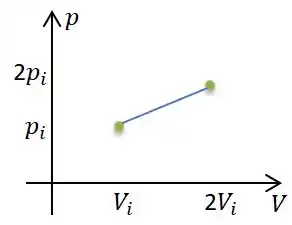
Agora é só calcular o volume abaixo dessa curva:
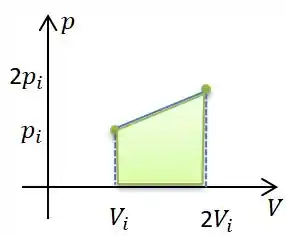
Passo 6
Esta área é a área de um trapézio, e de acordo com o nosso cálculo amado...
Onde é a base maior () e a base menor (), a altura é o tamanho , ou seja... . Como a área abaixo da curva representa a energia da transformação...
Essa é a energia expressa em termos de e .
Passo 7
Nesse problema daqui, precisamos buscar a energia requerida no processo para levar o gás de um estado para outro final. De acordo com a primeira Lei da Termodinâmica...
Onde é a energia interna da transformação. Essa energia, para os gases ideias pode ser dada por . Então...
Como ...
Porém no item vimos que...
Então...
Só que para os gases ideais
Então taí!
Resposta
Letra A:
Letra B:
Letra C:
Letra D: