Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Dilatação Térmica

Ver Teoria
Exercício 1912345678910111213141516171820212223242526272829303132333435

Enunciado

Duas berras retilíneas idênticas, bastante finas, de comprimentos L 0 são unidas por suas extremidades, formando um angulo de 90 ° entre si (veja figura ao lado). Ambas as barras tem coeficientes de dilatação linear dados por α .

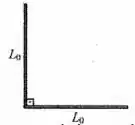
(a) (1,5) Se as barras são submetidas a uma variação de temperatura ∇ T >   0 , calcule a soma dos comprimentos das barras após este processo. Expresse seu resultado em termos de L 0 , α e ∇ T .

(b) (2,0) Calcule a variação de temperatura ∇ T > 0 a que deve ser submetida uma terceira barra, também de comprimento L 0 e de coeficiente de dilatação linear α para que as duas barras resultantes do processo descrito no item (a) e esta terceira barra formem um triangulo retângulo. Expresse seu resultado em termos de α e ∆ T .

Passo 1

L e t r a   A :

OPA! Ouvi falar em dilatação de barra? Ahhhh Meu querido então já anota aí que vamos utilizar a fórmula...

∆ L = α L 0 ∆ T

Onde ∆ L representa a variação do tamanho da barra ao ser aquecida no processo de dilatação.

Então podemos falar que ∆ L é a subtração do comprimento final L , pelo comprimento inicial L 0 ...

∆ L = L - L 0

Então, podemos falar que o comprimento final L de uma barra apenas vai ser...

L = L 0 + α L 0 ∆ T

Passo 2

Beleza! Mas o item a nos pediu o comprimento final das duas barras!

Uai! Se o comprimento final de uma barra é L = L 0 + α L 0 ∆ T , o comprimento de duas L idênticas vai ser...

L = 2 L     →

L = 2 L 0 + 2 α L 0 ∆ T

Passo 3

L e t r a   B :

POW! Esse item parece um pouco mais chato para a gente fazer sem desenhar, não acha? Então vamos fazer isso nesse passo, pode ser?

Inicialmente temos essas duas barras fazendo um ângulo de 90 ° ...

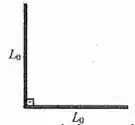
Depois de um tempo, com a aplicação da variação de temperatura ∆ T , essas barras se expandem para...

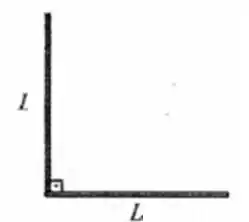
E no item B a gente quer encontrar a ∆ T ' que a gente vai ter que aplicar numa terceira Barra para ela formar ainda um triângulo retângulo com esse último esquema:

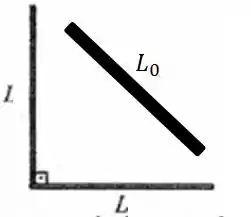
E aí? Como vamos resolver esse problema?

OBS: Cuidado para não confundirem ∆ T com ∆ T ' . ∆ T é a temperatura aplicada para aquecer as barras dos catetos (como no item a). Já ∆ T ' é a diferença de temperatura aplicada na barra 3 (hipotenusa) para ela dilatar ao ponto de se formar o triângulo retângulo, beleza?

Passo 4

Primeiro, vamos encontrar qual deve ser o tamanho que essa nova barra tem que atingir para cumprir este objetivo...

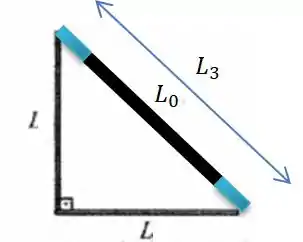
Esse tamanho L 3 aí é o tamanho que a barra L 0 deve atingir ao se aquecer com o ∆ T ' de temperatura que queremos determinar. Repare que pelo triângulo retângulo...

L 3 = L 2 + L 2     →

L 3 = L 2  

E esse tamanho L 3 tem é também pela dilatação a uma diferença de temperatura ∆ T ' , dada por...

L 3 = L 0 + α L 0 ∆ T '

Então...

L 2 = L 0 + α L 0 ∆ T '

Só que L = L 0 + α L 0 ∆ T pelos itens anteriores...

L 0 + α L 0 ∆ T   2 = L 0 + α L 0 ∆ T '

Para encontrar ∆ T ' basta isolar...

∆ T ' = L 0 + α L 0 ∆ T   2 - L 0 α L 0

Repare que podemos colocar L 0 em evidência...

∆ T ' = L 0 1 + α ∆ T   2 - 1 α L 0     →

∆ T ' = 1 + α ∆ T   2 - 1 α  

Resposta

Letra A:

L = 2 L 0 + 2 α L 0 ∆ T

Letra B:

∆ T ' = 1 + α ∆ T   2 - 1 α

Exercícios de Livros Relacionados

Determine a variação de volume de uma esfera de alumínio com um raio inicial de 10 c m quando a esfera é aquecida de 0 ° C para 100 ° C
A 20 ° C , uma barra tem exatamente 20,05 c m de comprimento, de acordo com uma régua de aço. Quando a barra e a régua são colocadas em um forno a 270 ° C , a barra passa a medir 20,11 c m de acordo c
Como resultado de um aumento de temperatura de 32 ° C , uma barra com rachadura no centro dobra pra cima . Se a distância fixa L 0 é 3,77 m e o coeficiente de dilatação linear da barra é 25.10 - 6 / °
Qual é o aumento de volume de um cubo de alumínio com 5,00c m de lado quando o cubo é aquecido de 10,0 ° C para 60,0 ° C ?
Três barras retilíneas de mesmo comprimento, feitas de alumínio, Invar e aço, todas a 20,0 ° C , formam um triângulo equilátero com pinos articulados nos vértices. A que temperatura o ângulo oposto à