Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Primeira Lei da Termodinâmica

Ver Teoria
Exercício 31123456789101112131415161718192021222324252627282930323334353637383940

Enunciado

A figura ao lado representa o diagrama pressão-volume de um ciclo termodinâmico que envolve um mol de um gás ideal que tem C v = 3 R / 2 , onde R é a constante universal dos gases.

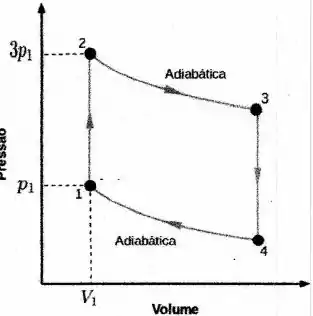
  1. i   Calcule as temperaturas nos pontos 1 e 2 e em seguida i i o calor trocado pelo sistema no processo 1 → 2 . Escreva suas respostas em i termos de p 1 , V 1 e R e em i i em termos de p 1 e V 1 .
  2. Calcule a variação da entropia para os processos 1 → 2 , 2 → 3 , 3 → 4 e de 4 → 1 .
  3. Sabendo que a eficiência da máquina térmica associada a tal ciclo é ε = 1 / 2 , calcule o trabalho por ciclo que ela realiza. Expresse sua resposta em termos de p 1 e V 1 .

Passo 1

Poxa! Olha que maneiro cara! Ao se observar o gráfico p V acima...

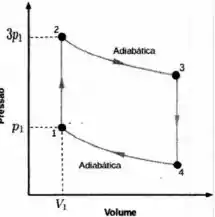
Observe que de 1 para 2 não há variação de volume V , o que nos leva a dizer que é um processo isocórico! Segura essa informação aí que ela vai ser muito útil no passo 3. Mas primeiro, vamos fazer o que se pede no subitem I da letra A, bora?

Passo 2

L e t r A - I t e m   I

Para então encontrar as temperaturas no ponto p 1 e no ponto p 2 , vamos nos lembra de que em um gás ideal é válida a relação...

p V = n R T

Como o enunciado nos disse, o número de mols no gás é n = 1   m o l , então...

p V = R T

Portanto, no ponto 1 ...

T 1 = p 1 V 1 R

E no ponto 2 ...

T 2 = p 2 V 1 R

Só que p 2 = 3 p 1 (olhando para o gráfico), então...

T 2 = 3 p 1 V 1 R

Passo 3

L e t r A - I t e m   I I

Agora temos que calcular o calor Q trocado no processo 1 → 2

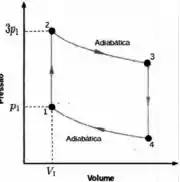
Pela 1 ª Lei da Termodinâmica, sabemos que...

Q = ∆ U + W

Onde ∆ U é a energia interna do sistema enquanto que W é o trabalho realizado pelo gás. Porém, todavia, contudo, não obstante... O trabalho no caso é nulo, pois não há variação de volume, ta ligado? Então...

Q = ∆ U

Essa energia interna ∆ U , para os gases ideias pode ser dada por ∆ U = n C v ∆ T . Então...

Q = n C v ∆ T

Pelo enunciado, n = 1 e C v = 3 R / 2 ...

Q = 3 2 R ∆ T

∆ T é a diferença de temperatura nos dois pontos máximos ( T 1 e T 2 )...

Q = 3 2 R T 2 - T 1     →

Q = 3 2 R 3 p 1 V 1 R - p 1 V 1 R     →

Q = 3 2 R 2 p 1 V 1 R     →

Então...

Q = 3 p 1 V 1

Passo 4

L e t r a   B :

POW! Podemos calcular a variação de Entropia ∆ S pela definição:

∆ S = ∫ T i T f d Q T

Então, para o processo de 1 → 2 ...

∆ S 12 = ∫ T 1 T 2 d Q T

Só que quem vem a ser d Q ?

Bem... No passo anterior, definimos Q = 3 2 R ∆ T , então d Q = 3 2 R d T ...

∆ S 12 = ∫ T 1 T 2 1 T ⋅ 3 2 R d T   →

∆ S 12 = 3 2 R ∫ T 1 T 2 1 T d T   →

Integrando...

∆ S 12 = 3 2 R ln ⁡ T T 1 T 2   →

∆ S 12 = 3 2 R ln ⁡ T 2 - ln ⁡ T 1   →

Por propriedade de logaritmo...

∆ S 12 = 3 2 R ln ⁡ T 2 T 1   →

Como T 2 = 3 T 1 pelo passo 2...

∆ S 12 = 3 2 R ln ⁡ 3

Agora veja que massa! O processo 3 → 4 é simétrico a esse processo 1 → 2 ...

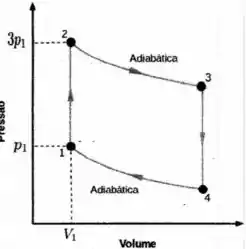
Só que o sentido negativo. O que nos leva a dizer que...

∆ S 34 = - 3 2 R ln ⁡ 3

BELEZA! Mas e os demais processos?

Passo 5

Bem... Para os demais processos (processo de 2 → 3 e 4 → 1 ) veja que são processos adiabáticos! E uma grande característica dos processos adiabáticos é de não terem variação de Q , ou seja, ∆ Q = 0 , portanto d Q = 0 também! Logo...

∆ S 23 = ∫ T 2 T 3 d Q T = 0                             e                           ∆ S 41 = ∫ T 4 T 1 d Q T = 0

Passo 6

L e t r a   D :

POW! Sabemos que a fórmula para a eficiência de uma máquina térmica pode ser dado pela razão entre o trabalho realizado por ela W e pela quantidade de calor absorvido para realizar esse processo.

ε = W Q a b s

Então, o trabalho será...

W = ε Q a b s   →

W = 1 2 Q a b s

O calor absorvido para a realização do trabalho acontece na etapa 1 → 2 , onde o processo aumenta a temperatura (e o calor é descartado nas etapas 3 → 4 ). E o calor absorvido já foi calculado no item A : Q a b s = 3 p 1 V 1 , então...

W = 3 p 1 V 1 2

Resposta

Letra A:

T 1 = p 1 V 1 R   ;                   T 2 = 3 p 1 V 1 R                 e               Q = 3 p 1 V 1

Letra B:

∆ S 12 = 3 2 R ln ⁡ 3 ;                 ∆ S 34 = - 3 2 R ln ⁡ 3 ;                       ∆ S 23 = 0                     e             ∆ S 41 = 0

Letra C:

W = 3 p 1 V 1 2

Exercícios de Livros Relacionados

Um atleta precisa perder peso e decide “puxar ferro”. (a) Quantas vezes um peso de 80,0k g deve ser levantado a uma altura de 1,00m para queimar 0,50k g de gordura, supondo que essa quantidade de gord
Use as condições e os processos mencionados no Problema 19.62 para calcular a) o trabalho realizado pelo gás, o calor fornecido ao gás e a variação de energia interna durante a expansão inicial; b) o
Em um processo adiabático envolvendo um gás ideal, (a) mostre que o módulo de elasticidade volumétrico é dado por B = - V d p d V = γ p Em que γ = C P / C V . (b) Mostre que a velocidade do som no gás
Um cano de comprimento L = 25,0m , aberto em uma das extremidades, contém ar à pressão atmosférica. O cano é introduzido verticalmente em um lago de água doce até que a água atinja metade da altura do
Calcule o trabalho realizado por um agente externo durante uma compressão isotérmica de 1,00m o l de oxigênio de um volume de 22,4L a 0 ° C e 1,00a t m para um volume de 16,8L .