2º EE de Física 3 da UFPE - 2018.1

Na figura abaixo, uma espira de corrente, que tem a forma de um triângulo equilátero de lado , é percorrida por uma corrente elétrica no sentido indicado. Um campo magnético uniforme , que ocupa todo o espaço, é aplicado ao longo do eixo , como esquematicamente representado na figura. Considere que os vetores unitários ao longo dos eixos , e , são respectivamente representados por  ,   e  . Nestas condições, calcule:

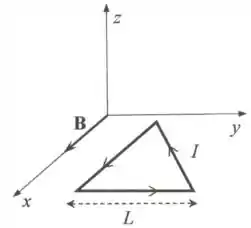
1. O vetor momento de dipolo magnético   da espira.
2. O vetor torque   que atua na espira.
3. A diferença de energia potencial magnética , se a espira passar de sua posição inicial mostrada na figura acima (associada à ), para uma posição final (associada à ) em que seu momento de dipolo magnético for paralelo ao campo magnético aplicado  . Observação: adote o nível de energia potencial magnética nula como aquele em que o vetor momento de dipolo magnético   é perpendicular ao vetor  .

A figura abaixo consiste de duas fontes (geradores) ideais e cinco resistores, cujos valores das respectivas forças eletromotrizes e resistências elétricas estão indicadas na figura. Para tal situação, calcule:

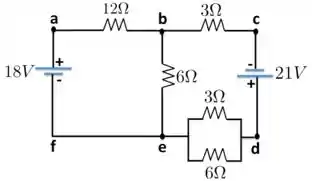
1. As correntes elétricas que fluem entre os pontos: e , e , e e .
2. As potências transferidas pelas duas fontes ideais.
3. A potência dissipada no resistor de resistência localizado entre os pontos e .

A figura abaixo ilustra um capacitor de placas metálicas esféricas de raios e , com . As placas são concêntricas e centradas na origem . O espaço entre as placas é completamente preenchido por uma substância não-condutora de constante dielétrica . Nas regiões restantes ( e ) há vácuo, onde é a distância radial até a origem . A constante de permissividade do vácuo é dada por .

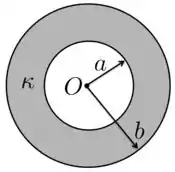
1. Calcule a capacitância do dispositivo usando a lei de Gauss, determinando a diferença de potencial entre as placas e finalmente aplicando a definição de capacitância.
2. Considerando que uma diferença de potencial é aplicada entre as duas placas metálicas, calcule a carga livre da placa interna.
3. Nas mesmas condições do item (b), calcule a carga ’ induzida na superfície do dielétrico que se encontra mais próxima da placa metálica interna.