A figura abaixo consiste de duas fontes (geradores) ideais e cinco resistores, cujos valores das respectivas forças eletromotrizes e resistências elétricas estão indicadas na figura. Para tal situação, calcule:
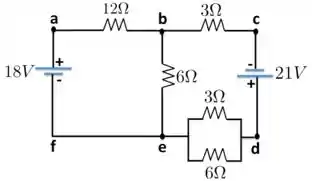
- As correntes elétricas que fluem entre os pontos: e , e , e e .
- As potências transferidas pelas duas fontes ideais.
- A potência dissipada no resistor de resistência localizado entre os pontos e .
Passo 1
Para resolvermos essa questão, vamos primeiro encontrar a resistência equivalente entre os pontos e na figura. Como esses resistores estão em paralelo, já que estão à mesma diferença de potencial, a resistência equivalente será:
Agora, vamos escolher (isso mesmo, você escolhe!!) os sentidos para as correntes e para as malhas. As malhas e foram escolhidas no sentido horário e as correntes e também no sentido horário, como desenhamos na figura abaixo. A corrente fluindo do ponto para o ponto .
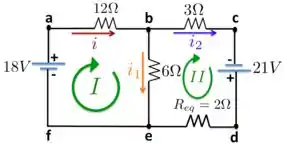
Uma vez que fizemos isso, vamos calcular os valores dessas correntes. Segue comigo aqui...
Passo 2
a) Neste passo, vamos encontrar os valores das correntes...
Nesse circuito, temos apenas dois nós, os pontos e . Aplicando a lei dos nós para o ponto , temos:
Agora, vamos aplicar a lei das malhas para as malhas e :
Para te ajudar a se lembrar de como utilizar a lei das malhas (“soma das ddp’s igual a zero”) que usamos para obter a equação acima, colocamos os seguintes passos:
- Como passa no o sentido do polo para o da fonte de , então o primeiro termo é: ;
- Como a corrente no resistor de está no mesmo sentido da malha , então há uma queda de potencial nesse resistor, por isso, acrescentamos o termo: ;
- No resistor de passa a corrente no mesmo sentido da malha , por isso, há uma queda de potencial nesse resistor e temos que adicionar o termo: .
Aplicando a ideia desses passos para a malha , temos a seguinte equação:
Das malhas e , obtemos, respectivamente, as seguintes expressões:
Substituindo isso na expressão que temos do nó :
que simplificada, resulta em:
Esse sinal negativo significa que sentido correto da corrente é o oposto ao indicado na figura.
Agora, para resolvermos o resto do sistema e encontrarmos e , mantemos o sinal negativo que encontramos para a corrente , ok? Usando esse valor para corrente, encontramos que
e
Passo 3
b) Continuando, agora podemos calcular as potências que cada uma das fontes de e transferem para o circuito.
A fonte de transfere:
A fonte de transfere:
Passo 4
c) A corrente que passa no resistor é . Por isso, a ddp entre os pontos e do circuito é:
Essa é a diferença de potencial para cada um dos resistores de e da associação em paralelo. Por isso, a corrente que passa no resistor de é:
A potência, então, que é dissipada nesse resistor é de: