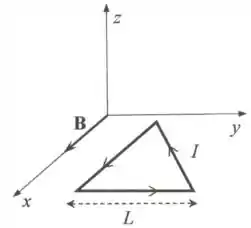
Na figura abaixo, uma espira de corrente, que tem a forma de um triângulo equilátero de lado , é percorrida por uma corrente elétrica no sentido indicado. Um campo magnético uniforme , que ocupa todo o espaço, é aplicado ao longo do eixo , como esquematicamente representado na figura. Considere que os vetores unitários ao longo dos eixos , e , são respectivamente representados por , e . Nestas condições, calcule:
- O vetor momento de dipolo magnético da espira.
- O vetor torque que atua na espira.
- A diferença de energia potencial magnética , se a espira passar de sua posição inicial mostrada na figura acima (associada à ), para uma posição final (associada à ) em que seu momento de dipolo magnético for paralelo ao campo magnético aplicado . Observação: adote o nível de energia potencial magnética nula como aquele em que o vetor momento de dipolo magnético é perpendicular ao vetor .
Passo 1
a) Aqui, a primeira coisa que precisamos saber é que o momento de dipolo magnético associado a espira é dado por:
sendo que é a área orientada da espira, que é sempre perpendicular à espira. A orientação desse vetor área é dado pela regra da mão direita. Nesta questão, como a corrente está no sentido anti-horário, se olhamos a espira por cima, pela regra da mão direita, o vetor área será
Agora, então, a gente precisa encontrar a área do triângulo equilátero da figura abaixo.
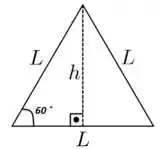
A altura desse triângulo pode ser obtida a partir do ângulo , como:
Portanto, módulo e , serão:
Para fechar, o momento de dipolo magnético da espira fica:
Passo 2
b) Como o campo magnético é uniforme, o torque sobre a espira é:
Como o produto vetorial , teremos:
Passo 3
c) Se o ângulo entre e é , então a energia potencial magnética é dada por:
Na situação inicial, o momento de dipolo magnético é perpendicular ao campo magnético e, por isso, . Então, como , a energia potencial magnética inicial será:
Na configuração final, é paralelo a , portanto, . Como , a energia magnética final será:
Com isso, a variação da energia potencial magnética é dada por: