A figura abaixo ilustra um capacitor de placas metálicas esféricas de raios e , com . As placas são concêntricas e centradas na origem . O espaço entre as placas é completamente preenchido por uma substância não-condutora de constante dielétrica . Nas regiões restantes ( e ) há vácuo, onde é a distância radial até a origem . A constante de permissividade do vácuo é dada por .
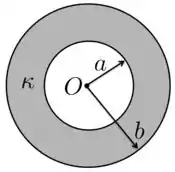
- Calcule a capacitância do dispositivo usando a lei de Gauss, determinando a diferença de potencial entre as placas e finalmente aplicando a definição de capacitância.
- Considerando que uma diferença de potencial é aplicada entre as duas placas metálicas, calcule a carga livre da placa interna.
- Nas mesmas condições do item (b), calcule a carga ’ induzida na superfície do dielétrico que se encontra mais próxima da placa metálica interna.
Passo 1
A primeira coisa que precisamos lembrar aqui é que a nova capacitância após a inserção do dielétrico com constante dielétrica é dada por:
sendo que é a capacitância no vácuo e é dada por
com sendo a diferença de potencial entre as esferas metálicas e o módulo das suas respectivas cargas, como mostra a figura abaixo.
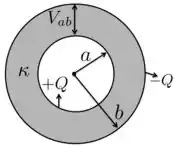
O potencial, por outro lado, a gente já viu que tem a seguinte equação:
em que é o elemento infinitesimal de caminho que está na direção radial e é o campo elétrico dentro da região .
Precisamos encontrar o campo elétrico nessa região, jogar na expressão para , resolver a integral e depois aplicar, no resultado, a definição de capacitância.
Bora lá?!!
Passo 2
a) Na figura abaixo, mostramos três gaussianas esféricas, , e .
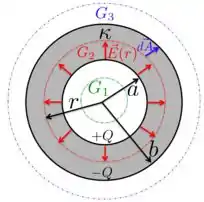
Vamos olhar primeiro as gaussianas esféricas e . Dentro da gaussiana não há nenhuma carga. Por isso, não tem campo elétrico na região , ou seja, . Já no interior da superfície gaussiana , a carga é dada por:
Agora, na região , onde temos a gaussiana esférica , temos que a carga líquida no interior dessa gaussiana é . Como essa carga é positiva, o campo elétrico que ela produz aponta saindo da superfície de raio e é paralelo ao vetor , como está desenhado na figura acima.
Além disso, o campo elétrico tem o mesmo valor em todos os pontos sobre a gaussiana esférica . Colocando tudo isso dentro da lei de Gauss, vamos ter o seguinte:
que dá um vetor campo elétrico na região dado por:
Passo 3
a) Continuação...
Para calcular o potencial , precisamos orientar o elemento radial . Vamos colocar esse elemento no mesmo sentido do campo elétrico que acabamos de encontrar, isto é, escrevê-lo como .
Quando a gente coloca isso dentro da expressão para e utilizamos o campo que encontramos no Passo 2, obtemos que:
Resolvendo essa integral, encontramos
Para fechar, então, a capacitância desse capacitor esférico quando ele é preenchido pelo dielétrico é:
Passo 4
b) A carga interna do capacitor é:
Passo 5
c) Quando colocamos o dielétrico dentro da região , o campo elétrico presente nessa região faz com que as cargas do dielétrico fiquem polarizadas: uma carga induzida negativa ’ se aproxima da carga positiva livre do capacitor e uma carga positiva ’ é induzida e se aproxima da carga livre negativa do capacitor, como mostra a figura abaixo.
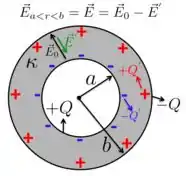
O campo elétrico gerado pelas cargas induzidas ’ e ’ se opõe ao campo elétrico criado pelas cargas livres e do capacitor. Por isso, o módulo do campo elétrico total na região é dado por:
Então, o campo inicial nessa região diminui quando o dielétrico é introduzido e a gente pode escrevê-lo como: , com . Jogando na expressão acima, o campo induzido é:
Mas podemos representar os campos elétricos e como:
Substituindo essas expressões naquela para , obtemos que a carga induzida vai ser:
em que utilizamos a expressão para obtida no Passo 4.