P2 de Física 3 da UNICAMP - 2020.2

ATENÇÃO: Ignorem o texto em inglês que se encontra nesse site, abaixo da figura. O que importa são as instruções fornecidas aqui. Utilizando os 2 últimos dígitos do RA do Aluno 1 (considerem que estes formam um único número de 2 dígitos; p. ex., se o RA é 123456, o número a ser usado será 56), calculem o valor da resistência a ser usado:

Tirem um print da tela mostrando a seleção da resistência na simulação e mostrem abaixo (podem selecionar o valor de 𝑅 na simulação o mais próximo possível do valor calculado):

a) Utilizando o gráfico da simulação calculem o valor da capacitância , descrevendo qual o procedimento utilizado. Tirem prints dos pontos selecionados do gráfico e colem estes na resolução de vocês.

Com a chave obrigatoriamente na posição open:

b) Deduzam a expressão da energia dissipada no resistor em função do tempo, partindo da equação da potência, .

c) Calculem a energia dissipada no resistor após um tempo , onde é a constante de tempo característica do circuito. Qual o valor da constante ? Qual o significado da constante ? Para o parâmetro , usem os últimos dígitos de seus RAs:

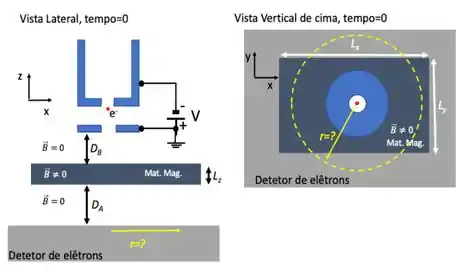
Um elétron é acelerado na direção com uma diferença de potencial e passa por uma abertura localizada a uma distância acima de um material magnético (Mat. Mag.) de dimensões , , , que possui um campo magnético interno . A uma distância do material magnético é colocado um detector de elétrons. As figuras mostram uma representação do arranjo experimental visto lateralmente (esquerda) e verticalmente (direita). Observem que as direções 𝑥, 𝑦 e 𝑧 foram pré-definidas nas figuras.

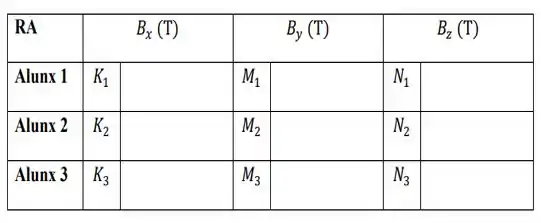
As componentes do campo magnético (medido em Teslas (T)) devem ser calculadas a partir dos seus RAs da seguinte maneira:

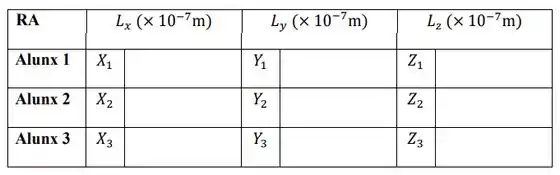
As dimensões do material magnético (medidas em metros (m)) devem ser calculados a partir dos seus RAs da seguinte maneira:

Por exemplo, se um estudante tiver , então . Caso algum valor de for , substituam por !

ATENÇÃO: Vocês trabalharão com conjuntos de valores de campo magnético e dimensões do material magnético, um conjunto para cada Alunx, como calculado nas tabelas acima.

Dados: Carga do elétron: ; massa em repouso do elétron: .

Para cada conjunto de valores de :

a) Determinem a distância em que o elétron será detectado no detector. Considerem que a variação de momento linear do elétron na direção 𝑧 desde a abertura até o detector é desprezível.

b) Se pudessem alterar a voltagem 𝑉, como ela afetaria a distância 𝑟 obtida? Considerando que as partes do aparelho não podem se mover mecanicamente, seria possível fazer com que os elétrons atingissem o detector no mesmo lugar, para os 3 conjuntos de valores? Explique.

c) As dimensões do material afetam de alguma maneira a distância 𝑟? Se sim, como?

A figura abaixo mostra um cilindro condutor muito longo de raio 𝑎, que possui uma densidade de corrente , e está circundado por uma camada cilíndrica condutora, de raio interno 𝑎 e raio externo 𝑏, que possui uma densidade de corrente , no sentido oposto da corrente do cilindro interno.

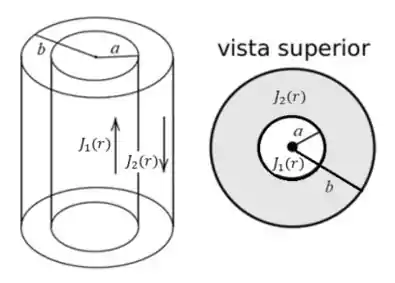
i. Usem os 2 últimos dígitos dos seus RAs (considerem que estes formam um único número de 2 dígitos; p. ex., se o RA é 123456, o número a ser usado será 56), para calcular o valor do parâmetro :

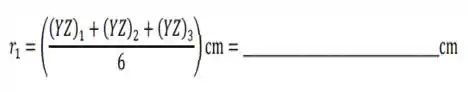
ii. Usem os 2 dígitos do meio dos seus RAs (considerem que estes formam um único número de 2 dígitos; p. ex., se o RA é 123456, o número a ser usado será 34), para calcular o valor do parâmetro :

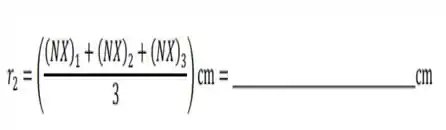
Usem o menor valor dentre e para ser o valor de 𝑎 e o maior para ser o valor de 𝑏. Caso , façam e (p. ex., se e , então e ; e caso , então e ).

iii. Usem os últimos dígitos dos seus RAs (p. ex., se o RA é 123456, o número a ser usado será 6) para obter:

iv. Usem os penúltimos dígitos dos seus RAs (p. ex., se o RA é 123456, o número a ser usado será 5) para calcular para calcular o parâmetro :

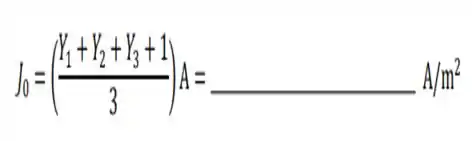
Resolvam os itens a seguir. Se necessário, usem . Não se esqueçam de detalhar todos os desenvolvimentos e não pular passagens.

a) Encontrem uma expressão algébrica para o módulo do campo magnético a uma distância 𝑟 do eixo do conjunto cilíndrico para . Depois, calculem o módulo do campo magnético para .

b) Encontrem uma expressão algébrica para o módulo do campo magnético a uma distância 𝑟 do eixo do conjunto cilíndrico para . Depois, calculem o módulo do campo magnético para .

c) Encontrem uma expressão algébrica para o módulo do campo magnético a uma distância 𝑟 do eixo do conjunto cilíndrico para . Depois, calculem o módulo do campo magnético para .

d) Há valores finitos de 𝑟 para os quais o campo magnético é zero? Se sim, quais? Justifiquem! Encontrem primeiro a expressão algébrica, e depois substituam os valores