A figura abaixo mostra um cilindro condutor muito longo de raio 𝑎, que possui uma densidade de corrente , e está circundado por uma camada cilíndrica condutora, de raio interno 𝑎 e raio externo 𝑏, que possui uma densidade de corrente , no sentido oposto da corrente do cilindro interno.

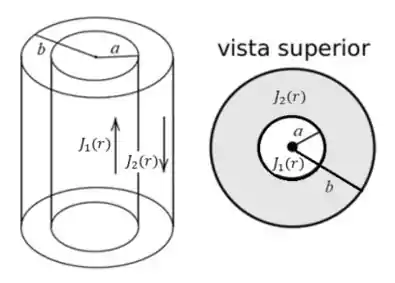
i. Usem os 2 últimos dígitos dos seus RAs (considerem que estes formam um único número de 2 dígitos; p. ex., se o RA é 123456, o número a ser usado será 56), para calcular o valor do parâmetro :

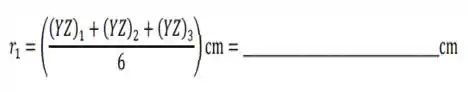
ii. Usem os 2 dígitos do meio dos seus RAs (considerem que estes formam um único número de 2 dígitos; p. ex., se o RA é 123456, o número a ser usado será 34), para calcular o valor do parâmetro :

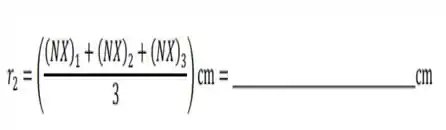
Usem o menor valor dentre e para ser o valor de 𝑎 e o maior para ser o valor de 𝑏. Caso , façam e (p. ex., se e , então e ; e caso , então e ).

iii. Usem os últimos dígitos dos seus RAs (p. ex., se o RA é 123456, o número a ser usado será 6) para obter:

iv. Usem os penúltimos dígitos dos seus RAs (p. ex., se o RA é 123456, o número a ser usado será 5) para calcular para calcular o parâmetro :

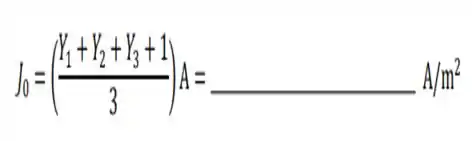
Resolvam os itens a seguir. Se necessário, usem . Não se esqueçam de detalhar todos os desenvolvimentos e não pular passagens.

a) Encontrem uma expressão algébrica para o módulo do campo magnético a uma distância 𝑟 do eixo do conjunto cilíndrico para . Depois, calculem o módulo do campo magnético para .

b) Encontrem uma expressão algébrica para o módulo do campo magnético a uma distância 𝑟 do eixo do conjunto cilíndrico para . Depois, calculem o módulo do campo magnético para .

c) Encontrem uma expressão algébrica para o módulo do campo magnético a uma distância 𝑟 do eixo do conjunto cilíndrico para . Depois, calculem o módulo do campo magnético para .

d) Há valores finitos de 𝑟 para os quais o campo magnético é zero? Se sim, quais? Justifiquem! Encontrem primeiro a expressão algébrica, e depois substituam os valores

Em seguida fazemos o mesmo para a casca externa:

Onde é a seção reta da casca cilíndrica externa. Temos que usar a mesma orientação da área de antes, senão nada faz sentido. O produto vetorial resulta:

Plugando na integral temos:

Integrando na casca cilíndrica externa obtemos sua área:

Vamos agora fazer um argumento genérico para todas as regiões de campo magnético e depois vamos só substituindo a corrente. Por se tratar de fios cilíndricos muito longos, temos uma simetria circular no campo magnético do problema.

Enunciando a Lei de Ampère:

Portanto escolhemos uma curva Amperiana circular de raio arbitrário . De forma que:

Em toda , o que implica:

Além disso temos que, pela configuração do campo, o módulo deste é constante em toda , portanto:

A integral de pedaços infinitesimais na Amperiana resulta no comprimento desta:

Como se trata de uma circunferência de raio , temos:

Como arbitramos tudo no sentido positivo de , basta multiplicar por para achar o sentido positivo do campo magnético. Quando a corrente for negativa ela já vai nos apontar o campo correto.

Agora a questão se resume a achar a corrente.

Na região , temos que a corrente interna é:

Onde nesse caso é o circulo de raio . Logo:

Logo o campo é:

Agora para a região temos que a única corrente é a do fio de raio que nós já tínhamos calculado na letra a, portanto:

Substituindo na equação de campo:

Para a região temos que a corrente interna tem contribuição tanto do fio de raio quanto da parte da casca que está dentro da Amperiana. Portanto:

Lembrando que a região entre e não tem corrente.

A corrente entre a casca externa e a Amperiana pode ser obtida pela integral (sério, até dá pra fazer sem a integral nesse caso pois é constante, mas se acostume a fazer com a integral que a chance de erro é bem menor):

Portanto a corrente interna é:

O campo então fica:

Por fim, a região pega somente a soma das correntes totais que tínhamos encontrado nas letras a e b: