P2 - Física III – Unicamp – Questão 1

Um elétron é acelerado na direção com uma diferença de potencial e passa por uma abertura localizada a uma distância acima de um material magnético (Mat. Mag.) de dimensões , , , que possui um campo magnético interno . A uma distância do material magnético é colocado um detector de elétrons. As figuras mostram uma representação do arranjo experimental visto lateralmente (esquerda) e verticalmente (direita). Observem que as direções 𝑥, 𝑦 e 𝑧 foram pré-definidas nas figuras.

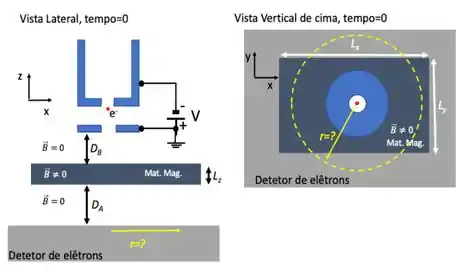
As componentes do campo magnético (medido em Teslas (T)) devem ser calculadas a partir dos seus RAs da seguinte maneira:

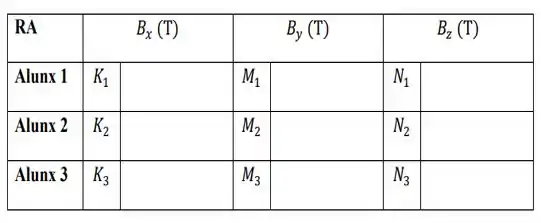
As dimensões do material magnético (medidas em metros (m)) devem ser calculados a partir dos seus RAs da seguinte maneira:

Por exemplo, se um estudante tiver , então . Caso algum valor de for , substituam por !

ATENÇÃO: Vocês trabalharão com conjuntos de valores de campo magnético e dimensões do material magnético, um conjunto para cada Alunx, como calculado nas tabelas acima.

Dados: Carga do elétron: ; massa em repouso do elétron: .

Para cada conjunto de valores de :

a) Determinem a distância em que o elétron será detectado no detector. Considerem que a variação de momento linear do elétron na direção 𝑧 desde a abertura até o detector é desprezível.

b) Se pudessem alterar a voltagem 𝑉, como ela afetaria a distância 𝑟 obtida? Considerando que as partes do aparelho não podem se mover mecanicamente, seria possível fazer com que os elétrons atingissem o detector no mesmo lugar, para os 3 conjuntos de valores? Explique.

c) As dimensões do material afetam de alguma maneira a distância 𝑟? Se sim, como?

Passo 1

Passo 2

Resposta