Calcule a integral
Passo 1
Opa, fala ai! Vamos continuar com nossos exercícios!
Deveríamos começar a questão pela integral de dentro, mas ela não parece muito simples em primeiro momento.
Vamos, então, tentar mudar essa ordem de integração para ver se a integral fica mais fácil. Mas não podemos apenas inverter as letrinhas ali não viu! Vamos com calma.
Primeiro, vamos esboçar a região em questão. Temos variando de a e entre e . Você não sabe desenhar a curva ?
Faça assim: substitua e na equação e encontre os valores correspondentes de (teremos e ).
Seu gráfico não precisa ficar perfeito, só precisamos saber que a região de integração tem essa cara:
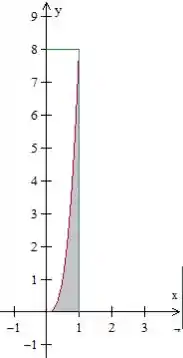
Passo 2
Agora vamos reescrever essa região como tipo I, lembrando que quando escrevemos a região do tipo I a gente quer que varie entre constantes e varie entre funções de .
Pelo próprio gráfico, vemos que varia entre e , portanto .
Já o valor de varia entre e a curva vermelha, vamos escrevê-la em função de (isolando o ):
Elevando os dois lados ao cubo, temos
E isso nos dá:
E assim nossa região de integração será:
Passo 3
Podemos, então, reescrever a integral da seguinte forma:
Nossa, bem mais tranquilo né? 😊
Passo 4
Vamos, agora, partir pra cima dessa integral!
Começando pela integral de dentro
Olhando só pra ela, temos:
Como estamos integrando isso em relação a , essa raiz funciona como uma constante e pode ser jogada pra fora da integral, ficando com
Agora podemos integrar, e isso nos dá:
Então nossa integral de dentro é
Passo 5
Vamos pegar esse resultado e aplicar na integral de fora, ficando com
Para resolver essa integral, não se assuste! Vamos usar o nosso método de substituição simples e vamos falar que:
Derivando dos dois lados, temos que
Então ficamos com
Simplificando isso temos
Passo 6
Agora, para não termos que ficar indo e voltando com a substituições, podemos acertar os limites de integração para ficar em função de
Temos que quando (nosso limite inferior)
E quando (nosso limite superior)
Passo 7
Então nossa integral passa a ser:
Podemos tirar o da integral por ser uma constante, e ficamos com
Aqui vamos lembrar que . Integrando em relação a , temos:
Substituindo os limites temos:
Que nos dá
E encontramos o resultado da nossa integral.