Calcule a integral dupla
Em que é a região plana:
Passo 1
Opaaa, fala ai!! Vamos continuar nossos estudos para ficar fera na matéria!
Para resolver essa integral, precisamos saber os limites de integração! Para isso, vamos dar uma olhada na região ?
As desigualdades nos dizem que e são maiores ou iguais a , e que , ou seja, é menor ou igual a reta . Juntando tudo temos:
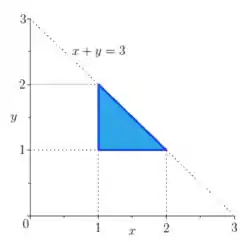
Para interpretar essas desigualdades é legal colocar o dedo sobre a curva e ver o que temos: colocando o dedo sobre a reta , deve ser menor do que ela, então andamos para baixo dela! E, como e são maiores ou iguais a , estamos em cima de e a direita de ;)
Passo 2
Agora, podemos ver os limites de integração da integral dupla!
Como a reta , pode ser escrita como , temos que é função de , logo, devemos integrar antes em relação a . Além disso, vemos que Como quando temos (vértice direito do triângulo), temos que . Colocando esses limites na integral, fica:
Passo 3
Pronto! Agora só precisamos resolver a integral ;) E o que temos é:
Passo 4
Vamos começar com a integral de dentro, em relação a :
Vamos fazer uma substituição simples
Trocando o para na nossa expressão inicial, temos
Substituindo os limites de integração na variável que acabamos de integrar, ficamos com
Como nossos expoentes são negativos, não podemos fazer as contas com eles assim, então vamos jogar eles pra baixo pra deixá-los positivos. O que nos dá:
Passo 5
Show, agora vamos pegar esse resultado e aplicar na integral de fora!
Agora vamos separar em duas integrais
Pra resolvermos a segunda integral precisaremos fazer uma substituição simples. Então, vamos chamar e vamos ter que
Integrando, teremos:
Lembrando que , ficamos com:
Substituindo os valores dos limites na expressão, temos:
Aqui vamos tirar o m.m.c., pois precisamos que os denominadores sejam iguais:
Agora sim. Somando tudo, temos:
Pronto! Integral resolvida!