Use integral dupla para calcular a área da região limitada por:
No primeiro quadrante.
Passo 1
Opaa fala aii! Vamo que vamo, senta ai, respira fundo e simbora pra nossa questão!
Quando a gente quer calcular uma área através da integral dupla, nós fazemos a integral na região da seguinte forma:
Fazendo um esboço da nossa região, nós temos duas retas: , ; e um gráfico mais estranho: , que vamos escrever como .
ps. Como ele só quer a parte no primeiro quadrante, temos algo assim:
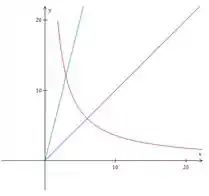
Não dá pra escrever a região nem como tipo , nem como tipo , diretamente, então vamos ter que separar em dois pedaços e , mas calma que não é nada demais, você vai ver...
Passo 2
O primeiro pedaço vai ser até a reta de cima encontrar com a curva .
Pra achamos o valor de quando isso acontece, nós igualamos as duas funções, assim acharemos o ponto de interseção entre as duas. Vamos ter algo assim:
Isso nos dá que
Simplificando temos que
Então, podemos concluir que:
Maaaaaaaaaas como estamos no primeiro quadrante, nosso tem que ser positivo!
Então a região é assim:
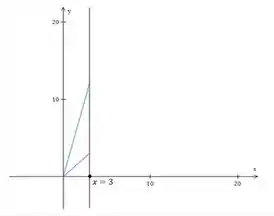
A integral vai ser assim, então:
Passo 3
Calculando a integral que encontramos no passo anterior:
Começando com a integral de dentro, ficamos com
Isso nos dá
Substituindo pelos limites de integração temos
Que nos dá
Aplicando isso na integral de fora, ficamos com
Ficando assim
E enfim, chegamos à área desse primeiro pedaço.
Agora só falta o outro pedaço!
Passo 4
O pedaço que estava faltando era:
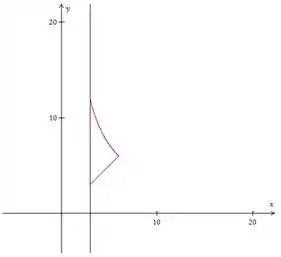
Que também é tipo , então vamos achar o ponto que a reta de baixo encontra a curva pra saber até onde vamos integrar em :
Igualando a função de baixo (), com a função de cima (:
Como estamos no primeiro quadrante, temos que:
E a integral fica, então:
Passo 5
Agora é só calcular a integral:
Resolvendo a integral de dentro, em :
Isso fica
Substituindo os valores, temos:
Vamos lembrar que vamos ficar com:
E esse é o cálculo que representa a área do nosso segundo pedaço da região.
Passo 6
Agora é só somar tudo!!
Lembrando que
E que a nossa área é calculada fazendo a soma deles:
Então ficamos com: