Suponha que uma lâmina com densidade ocupe a região do plano . Calcule a massa total sabendo que é a região triangular de vértices e a densidade em cada ponto é igual à distância de ao eixo
Passo 1
Oie. Enunciado esquisito né? Mas vamos no passo a passo.
Pela definição de cálculo de massa por integrais duplas, podemos achar a massa de uma lâmina fazendo a seguinte integral:
Portanto, para resolver esse problema, a primeira coisa que vamos precisar é determinar os limites de integração da nossa região ! Depois é só jogar na integral, beleza? Vamos ver como!
Passo 2
O exercício diz que a nossa região é um triângulo com os vértices certo? Com essa informação vamos ter que achar as retas associadas a esses pontos. No gráfico fica assim:
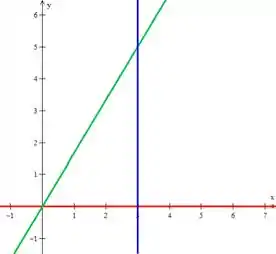
Perceba também que, quando ele fala que a densidade é igual a distância de cada ponto P ao eixo , o que ele está nos falando é que a densidade será igual a coordenada de desses pontos. Isso porque é essa coordenada que dá exatamente a distância do ponto ao eixo .
Ficou confuso? Olha esse exemplo:
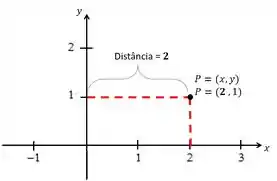
Então, a densidade será escrita como:
Então, no final das contas, quem a gente realmente quer calcular é:
Passo 3
Agora que está tudo mais claro, vamos desenvolver o nosso problema. No nosso gráfico temos três retas delimitando a região , duas são mais fáceis de visualizar:
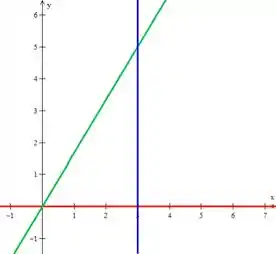
A terceira dá para descobrir qual é! Sabemos que ela passa pelos pontos e , né? Então é vamos usar a equação de reta:
Como temos dois ponto, vamos substituir cada um deles na equação da reta e assim vamos encontrar os coeficientes e .
No ponto (0,0):
No ponto (3,5):
Logo, substituindo e na equação original:
Passo 4
Vendo o gráfico pelo tipo I, concluímos que os limites de integração são:
Substituindo os valores calculados na integral temos:
Passo 5
Resolvendo a integral, começamos pela integral de dentro:
Substituindo os limites de integração:
Agora vamos resolver a integral que sobrou:
E assim encontramos a massa total da lâmina.