(Adaptado) Um equipamento para recuperação de calor envolve a transferência de energia dos gases quentes de exaustão, que passam através de uma região anular, para água pressurizada que escoa através do tubo interno da região anular.
Esse tubo interno possui diâmetros interno e externo de e e comprimento igual a , e está conectado a um tubo externo, isolado termicamente da vizinhança e com de diâmetro, por meio de oito barras de suporte.
Cada barra de suporte possui de espessura e é fabricada formando um conjunto integrado com o tubo interno em aço carbono .
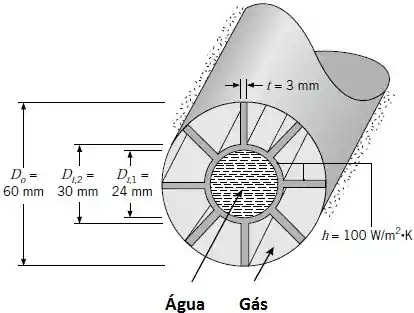
Considere condições nas quais a água a escoa através do tubo interno a uma vazão de , enquanto os gases de exaustão a escoam através da região anular, mantendo um coeficiente convectivo de sobre as superfícies das barras de suporte e a superfície externa do tubo interno.
Qual é a taxa de transferência de calor do gás para a água?
Passo 1
A taxa de transferência de calor será dada por:
Onde, como temos um problema com aletas para o escoamento externo e sem fatores de deposição, o produto será dado por:
Vamos trabalhar com cada termo separadamente, beleza?
Passo 2
Para o termo de convecção interna, de acordo com a tabela A.4, considerando a temperatura de , temos as seguintes propriedades da água:
Assim, o número de Reynolds será:
Como temos um escoamento turbulento, a correlação mais adequada para o número de Nusselt, será:
Assim, o coeficiente convectivo será dado por:
Finalmente, o termo de convecção interna será:
Passo 3
Para o termo de condução, como estamos trabalhando com uma geometria cilíndrica, teremos:
Substituindo os valores:
Passo 4
Para o termo de convecção externa, teremos:
Como o problema já nos deu o coeficiente convectivo, temos apenas que calcular a eficiência global da superfície, dada por:
Onde:
Onde é o comprimento da aleta e é a sua altura.
Obs.: Multiplicamos a área por 8 pois são oito aletas, e por 2 pois estamos trocando calor com os dois lados da aleta.
Assim, a eficiência global da superfície será:
Logo:
Passo 5
Substituindo na expressão do coeficiente global de transferência de calor:
Passo 6
Assim, a taxa de transferência de calor será:
![]()