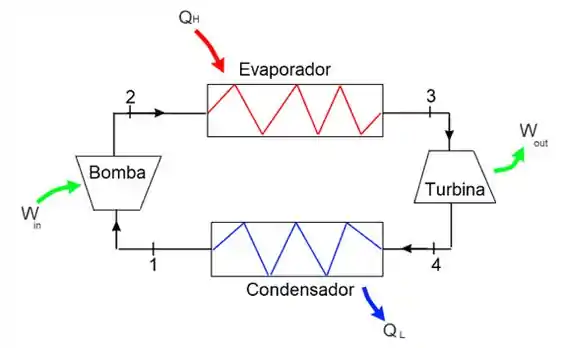
Um motor térmico opera segundo um certo ciclo termodinâmico, representado abaixo. Calcule a potência deste ciclo sabendo que a vazão mássica do fluido de trabalho é igual a . Considere que os processos no evaporador e no condensador são isobáricos e na bomba e turbina adiabáticos.
Passo 1
Para resolver esse problema a gente tem que lembrar que a diferença de entalpia num processo isobárico é igual ao calor transferido. Portanto:
Aqui vale a observação de que estamos utilizando os calores específicos e porque foi fornecida a entalpia específica .
Passo 2
Calcular os calores específicos:
Passo 3
Aplicando a primeira lei para ciclos:
Passo 4
Mas a gente acabou de calcular o trabalho específico, para achar a potência basta multiplicar pela vazão mássica de :
Resposta
Exercícios de Livros Relacionados
Um condicionador de ar produz um efeito de resfriamento de 2 kW enquanto rejeita 2,5 kW de calor. Qual é o seu COP?
Um sistema de refrigeração deve resfriar uma massa média de 350 g de pães a partir de uma temperatura inicial de 30 °C até -10 °C, a uma taxa de 1.200 pães por hora, utilizando ar refrigerado a -30 °C
A substituição de lâmpadas incandescentes por lâmpadas fluorescentes de baixo consumo reduz o consumo de energia de iluminação a 1/4 do que era anteriormente. A energia consumida pelas lâmpadas e, no
Compare a eficiência térmica de uma turbina a gás de dois estágios com regeneração, reaquecimento e resfriamento intermediário à eficiência de uma turbina a gás de três estágios com o mesmo equipament
Um novo refrigerador doméstico típico consome cerca de 680 kWh de eletricidade por ano e tem um coeficiente de performance de 1,4. A quantidade anual de calor removida do espaço refrigerado por esse r