Determine analisando triângulo abaixo qual é o valor da soma das medianas.
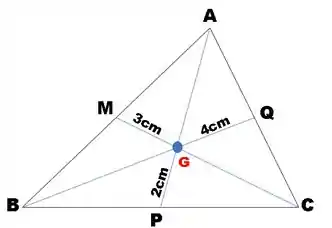
Passo 1
Existe uma propriedade das medianas de um triângulo que garante que o ponto (Baricentro), divide a mediana em duas partes.
A menor dessas partes tem comprimento vezes menor que a parte maior.
Logo,
Passo 2
Como temos os valores dos lados menores das medianas, basta multiplicar por dois para descobri o valor dos lados maiores:
1º Mediana
A soma entre e resultará no comprimento total da mediana :
2º Mediana
A soma entre e resultará no comprimento total da mediana :
3º Mediana
A soma entre e resultará no comprimento total da mediana :
Passo 3
Agora basta somarmos as três medianas para obter o valor total:
Resposta
centímetros .