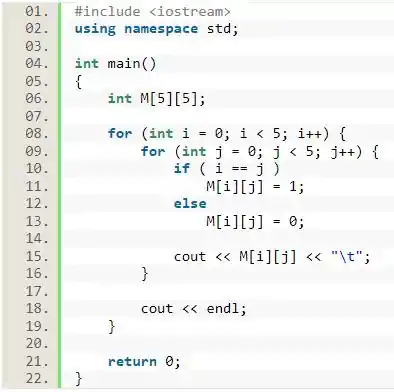
Declare uma matriz 5 x 5. Preencha com 1 a diagonal principal e com 0 os demais elementos. Escreva ao final a matriz obtida.
Passo 1
Fala aí, tudo tranquilo?
Para essa questão, nós vamos iniciar declarando a matriz. Como ela recebe somente valores inteiros, podemos declará-la como . Dessa forma, temos:
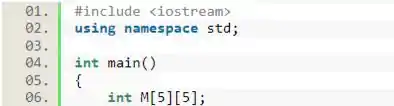
Além disso, como vamos ter que imprimir os valores da matriz, perceba que já fizemos a inclusão da biblioteca .
Passo 2
A seguir, nós temos que acrescentar os valores a essa matriz. Como esses valores possuem um padrão bem definido, é interessante fazermos um laço de for para ir acrescentando cada valor de acordo com a condição de se o valor está na diagonal principal (os índices das posições forem iguais) ele será 1, caso contrário, ele será 0.
Para passarmos por todos os valores dessa matriz, é importante que façamos dois laços de . O primeiro para variar o índice das linhas e o segundo, interno ao primeiro, para variar o índice das colunas. Dessa forma, podemos ir preenchendo todos valores indo de linha por linha.
![]()
Agora, basta usarmos e para as condições que colocamos que definimos.
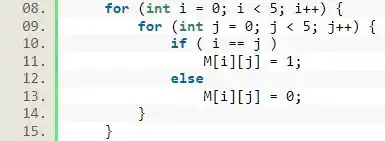
Passo 3
Para finalizar, basta printarmos todos os termos dessa matriz. Para fazer isso, temos que usar do mesmo esquema de laços de , passando por todos os termos da matriz e usando a função . Isso é algo muito bom, pois podemos aproveitar o laço de for que já fizemos e apenas acrescentar o comando para imprimir o valor após ele ser passado para a matriz:
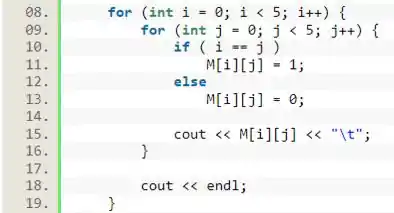
Perceba que usamos o comando de imprimir duas vezes. Uma dentro do que varia a coluna, na linha 15, e outro dentro apenas do que varia a linha, na linha 18 do código. O primeiro serve para imprimirmos o valor e dar uma distância entre valores da mesma coluna, usando o . O segundo serve para fazermos uma quebra de linha no momento em que mudamos para a próxima linha da matriz, melhorando a nossa organização no momento de imprimir a matriz.
Resposta