Translação de Corpos Rígidos
Teoria
Introdução
Você já reparou no movimento de um elevador?
Ele só sobe ou desce, não é mesmo? Então, podemos dizer que o elevador realiza um movimento de translação. Mas o que tem de especial neste tipo de movimento?
É o que vamos ver neste capítulo...
Partiu?
Translação
Nós vimos que um corpo realiza um movimento de translação sempre que todos os pontos que pertencem ao corpo se deslocam em trajetória paralelas. Essas trajetórias podem ser retas ou curvas:
- Quando a trajetória é reta dizemos que ocorreu uma translação retilínea:
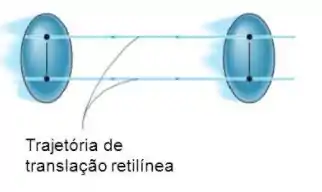
- Quando a trajetória é uma curva dizemos que ocorreu uma translação curvilínea:
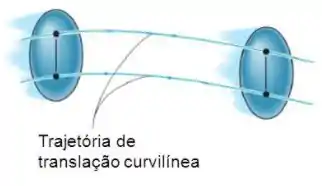
Antes de analisar o movimento de translação de um corpo rígido, vamos fazer uma breve revisão de movimento relativo de dois corpos.
Revisão de Movimento Relativo
Imagine dois corpos e se movendo. O que queremos saber é o movimento que faz com relação ao corpo . Para isso, temos que nos posicionar sobre o ponto e bisbilhotar tudo que está fazendo. Mas como fazemos isso mesmo?
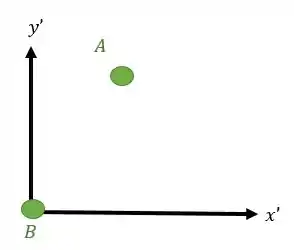
Temos que posicionar um eixo móvel (pois o eixo se move junto com o ponto) bem em cima do ponto . É esse eixo que vai servir para bisbilhotarmos o ponto ! 
Agora, vamos marcar neste eixo a posição do corpo medido com relação ao corpo :
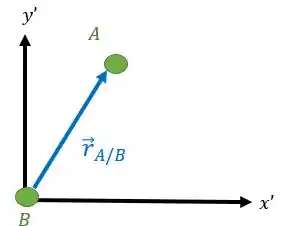
Dizemos que é a posição relativa entre e . Este vetor indica como o corpo está posicionado quando você o observa a partir do ponto . Observe que o vetor começa na origem do eixo móvel e chega no ponto que estamos analisando que é o corpo .
Agora, precisamos achar a posição absoluta ( e ) de ambos os corpos com relação a um eixo fixo (que vamos chamar de eixo absoluto ) localizado em um ponto de referência fora dos corpos e .
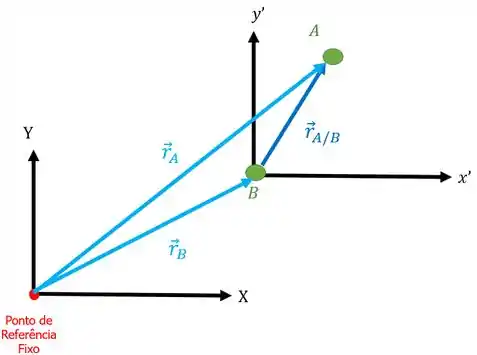
Perceba que os vetores e começam na origem do eixo absoluto e chegam no respectivo ponto.
Agora, vamos fazer a soma vetorial desses vetores. Se tirarmos os eixos, vamos ter:
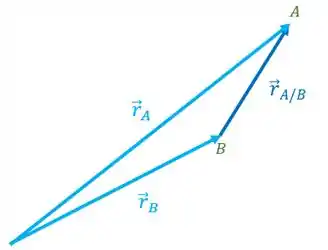
Então, podemos escrever a seguinte equação:
O que essa equação nos diz? Que a posição absoluta do corpo é igual a posição absoluta do corpo mais a posição relativa de com relação a .
Beleza!!!
Mas e a velocidade desses corpos? É só lembrar que a velocidade é a derivada da posição com relação ao tempo, então...
Isso quer dizer que a velocidade do corpo é igual a velocidade do corpo mais a velocidade do corpo com relação a .
E a aceleração em? Só fazermos o mesmo procedimento e derivarmos a equação da velocidade com relação ao tempo:
Não se esqueça que:
Lembrou de movimento relativo quando temos dois corpos se movendo? Agora vamos ver o movimento relativo em um corpo rígido único.
Translação de Corpo rígido
- Posição: vamos imaginar um corpo rígido realizando movimento de translação e vamos pegar uma canetinha e marcar nele dois pontos e que pertencem a este mesmo corpo:
- Velocidade: para obter a velocidade dos pontos e é só derivarmos a equação da posição que acabamos de achar com relação ao tempo:
- Aceleração: derivando com relação ao tempo a equação da velocidade, vamos obter a aceleração:
A localização dos pontos e vão ser definidas por vetores posição e que começa na origem do eixo absoluto (que é aquele fora do corpo) e termina em seu respectivo ponto:
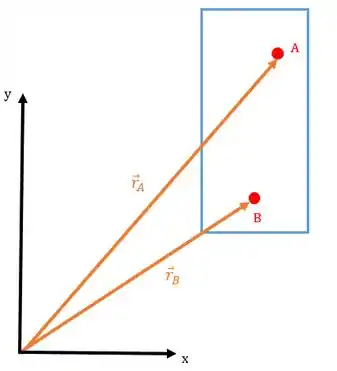
Agora vamos colocar um eixo fixo no corpo e com a origem no ponto :
Feito isso, podemos localizar o vetor posição do ponto com relação a que é o vetor posição relativa :
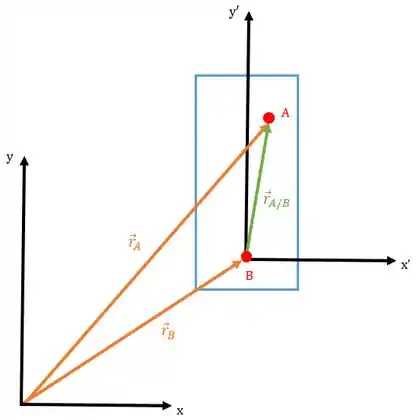
Fazendo adição desses vetores obtemos:
Como os pontos e pertencem ao mesmo corpo rígido, a distância entre eles é a mesma sempre.
E já que ele está realizando um movimento de translação, o módulo e o sentido do vetor é constante, de modo que sua derivada é zero. Então, vamos ter:
Essas equações indicam que todos os pontos de um mesmo corpo rígido que está realizando um movimento de translação seja retilínea ou curvilínea, têm a mesma velocidade e a mesma aceleração.
Vamos fazer uns exercícios? Então, bora! 
Translação
Revisão de Movimento Relativo
Translação de Corpo rígido
Exercícios Resolvidos
Exercício Resolvido #1
R. C. Hibbeler, Dinâmica: Mecânica para Engenharia, 10º ed. SP: Prentice Hall, 2005, pp. 76-12.196
Dois aviões, e , voam à mesma altitude. Suas velocidades são e , respectivamente, e seus cursos retilíneos formam um ângulo . Determine a velocidade de em relação à aeronave .
Passo 1
Nosso primeiro passo é localizar os vetores , e . Repare que o vetor velocidade de em relação à aeronave começa no ponto e chega no ponto :
Sabemos que velocidade relativa é:
Então:
Passo 2
Nosso próximo passo é decompor os vetores e no eixo :
Temos que:
E:
Beleza!
Passo 3
Agora é só somar componente com componente e componente com componente :
Vamos achar o módulo do vetor velocidade relativa de com relação à usando teorema de Pitágoras:
Resposta
Exercício Resolvido #2
J.L. Meriam e L.G. Kraige, Mecânica para Engenharia, Estática, 6º ed. RJ: LTC, 2012, pp. 71-2/199.
O navio está se dirigindo para o oeste a uma velocidade de , e o navio está se dirigindo para o sudeste. A direção relativa de com relação a é de 20° e é invariável. Se a distância entre e é de às , quando a colisão ocorreria se nenhum navio alterasse o curso?
Passo 1
Para começar vamos fazer um esquema com os vetores:
Sabemos que:
Mas não temos os valores da velocidade e nem da velocidade relativa . Então, vamos aplicar a lei dos senos. Para isso, temos que descobrir os ângulos entre os vetores.
Repare que o ângulo entre duas direções da Rosa dos Ventos é de 45°:
Então, nosso esquema de vetores fica da seguinte forma:
O ângulo entre a direção oeste e a direção sudeste é de 45°. Fica bem mais fácil achar o valor de e de agora:
Passo 2
Beleza! Agora que sabemos os ângulos vamos fazer a lei dos senos:
Uma coisa importante: 1 nó é igual a uma milha marítima por hora!
A questão quer saber o horário da colisão, não é mesmo? Nós temos a distância entre os barcos que é de e temos a velocidade relativa, então:
O tempo inicial é , então temos que acrescentar :
A colisão ocorre às 14h e 24 min!
Resposta
Exercício Resolvido #3
J.L. Meriam e L.G. Kraige, Mecânica para Engenharia, Estática, 6º ed. RJ: LTC, 2012, pp. 71-2/203.
O carro está viajando na velocidade constante de enquanto contorna a curva circular com de raio e no instante representado está na posição . O carro está viajando na velocidade constante de e passa pelo centro do círculo neste mesmo instante. O carro é localizado em relação ao carro pelas coordenadas polares e com o pólo se deslocando com . Para esse instante determine e os valores de e conforme medidos por um observador no carro .
Passo 1
O primeiro passo nesse tipo de questão é localizarmos os vetores velocidade de cada carro:
Podemos juntar os vetores e de modo a construir um triângulo:
Repare que como queremos o vetor velocidade relativa de com relação a (), então ele deve começar no ponto e chegar até o ponto .
E qual vai ver o ângulo ? É a soma do ângulo que tem entre o vetor e o raio com o ângulo que tem entre o raio e o vetor :
Agora vamos aplicar a lei dos cossenos:
Passo 2
Como o raio é dado em metros, vamos passar as velocidades para e para isso, é só dividir por 3,6:
Nosso próximo passo é calcular as componentes da velocidade na coordenada polar que são as componentes radial e tangencial da velocidade relativa .
Nas coordenadas polares temos duas componentes para a velocidade:
Vamos ver como fica a coordenada polar na situação inicial do nosso exercício:
Repare que o vetor tem a mesma direção e sentido do vetor , então vamos achar o ângulo entre os vetores e :
Para isso, vamos usar a lei dos senos:
Passo 3
Vamos colocar o ângulo no nosso esqueminha:
Agora, é decompor o vetor :
Mas lembra que:
Então:
E para ? É só decompor na outra direção:
Temos que:
Então:
O sinal de menos é porque o vetor está no sentido contrário do eixo da coordenada polar:
Resposta
Exercício Resolvido #4
R. C. Hibbeler, Dinâmica: Mecânica para Engenharia, 10º ed. SP: Prentice Hall, 2005, pp. 76-12.197
Num dado instante, os carros e trafegam a velocidades de e , respectivamente. Se tem sua velocidade aumentada a uma taxa de , enquanto se mantém com velocidade constante, determine a velocidade e a aceleração de em relação a , nesse instante.
Dados: o raio da curva é ;
Passo 1
Como ele quer a velocidade de em relação a , o que temos que fazer é nos posicionar em e observar tudo que está fazendo. Vamos ter o seguinte:
Você pode estar se perguntando por que não coloquei o vetor começando em cima do carro . É porque o carro está se movimentando ao longo de uma reta, então posso posicionar o vetor em qualquer ponto ao longo da reta. Beleza?
Sabemos que:
Portanto, podemos escrever:
Passo 2
Para descobrir é só acharmos as componentes de e nos eixos :
Então:
E ?
Antes de calculá-lo, vamos trabalhar com aquele ângulo dado no enunciado:
Assim:
Vamos fazer a soma vetorial agora:
Como a questão pediu o módulo da velocidade relativa, é só aplicarmos o teorema de Pitágoras:
Passo 3
E a aceleração? O carro realiza um movimento retilíneo e sabemos que no movimento retilíneo a aceleração é calculada derivando a velocidade com relação ao tempo:
Como a velocidade do carro é constante, então:
O carro realiza um movimento curvilíneo, então a sua aceleração pode ter duas componentes: uma tangencial e responsável por mudar o módulo da velocidade e uma centrípeta responsável por mudar a direção.
Como no enunciado foi dito que a velocidade do carro aumenta a uma taxa de , já sabemos a componente tangencial da aceleração.
Como a velocidade do carro aumenta, então o vetor tem o mesmo sentido e direção do vetor .
Sabendo que o raio da curvatura é , a aceleração centrípeta vai ser calculada assim:
O vetor sempre aponta para o centro da curva!
Vamos ter o seguinte esquema:
Passo 4
Queremos saber a aceleração de em relação a , não é mesmo? Então:
Vamos isolar o que queremos:
Agora, temos que decompor os vetores aceleração no eixo como fizemos antes com a velocidade.
O vetor terá a mesma decomposição do vetor , já que tem a mesma direção e mesmo sentido do mesmo:
O vetor ficará assim:
Então, a decomposição será:
O vetor aceleração do carro será:
Passo 5
Calma, já está quase acabando! Vamos substituir as acelerações de cada carro na equação da aceleração relativa:
Então:
Agora, vamos calcular o módulo da aceleração: