Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 6.3 - Ex. 23
O carrinho se desloca para a direita com aceleração . Se o deslocamento angular constante da haste essbelta uniforme de massa foi verificado ser de , determine o valor da constante contorcional da mola. A mola, que exerce um momento de módulo sobre a haste, está se deformação quando a haste está vertical. Os valores de e são e , respectivamente. Considere a pequena esfera de massa na extremidade como uma partícula.
Passo 1
Vamos começar calculando o momento da força resultante agindo sobre a haste e sobre a bola presa na sua extremidade. As forças são:
E as forças agem no centro de massa de cada objeto. Vamos fazer um diagrama para calcular o momento delas em relação a um ponto conveniente para nós:
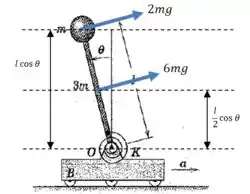
E então os momentos dessas forças resultantes são:
Essas duas quantidades são os momentos resultantes do sistema.
Passo 2
Ok, já temos o momento resultante, então a soma dos momentos das forças que agem sobre o sistema é:
Quais são as forças que produzem esse momento? Temos os pesos e , e o momento gerado pela mola:
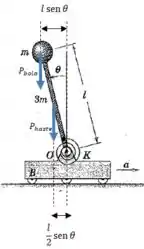
E o sinal negativo aparece nos momentos dos pesos porque eles favorecem a rotação no sentido contrário ao das nossos momentos resultantes.
Passo 3
Agora ficamos com a seguinte equação:
E nosso objetivo é calcular , então vamos isolar nessa igualdade:
Agora é só substituir os valores numéricos, lembrando que , quando aparece sozinho, deve estar em radianos:
Resposta
A constante contorcionai da mola é .