Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 6.3 - Ex. 19
Determine o módulo e a direção da força necessária para transmitir uma aceleração para trás ao carrinho de mão carregado, sem rotação a partir da posição mostrada. A massa combinada do carrinho de mão e de sua carga é com o centro de massa em . Compare a força normal em sob aceleração com aquela para equilíbrio estático na posição mostrada. Despreze o atrito e a massa da roda.
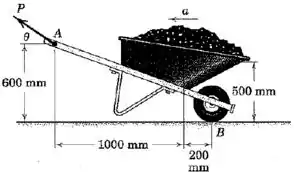
Passo 1
Vamos começar calculando a força normal em no caso em que o carrinho está em equilíbrio estático na posição da figura. Isso já vai nos ajudar a responder as outras perguntas.
Precisamos de um esquema da situação:
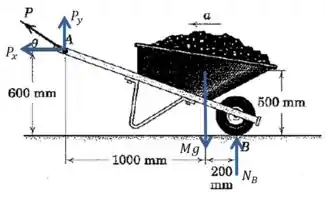
Para que o sistema esteja em equilíbrio, os momentos das forças precisam se cancelar. Vamos então calcular o momento total em relação ao ponto :
Por que o ponto ? Porque dessa forma vamos sumir com o momento da força , que é desconhecida, e vai sobrar apenas e :
E o sinal negativo aparece em porque ela favorece rotação no sentido horário.
Beleza, essa é a força normal no caso estático.
Passo 2
Agora vamos analisar essa mesma força no caso em que há movimento. O que muda nesse caso?
Como agora o carrinho de massa tem aceleração , nós temos uma força resultante . Qual é o momento dessa força resultante em relação ao ponto ?
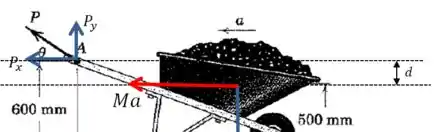
Ok, então a soma dos momentos das forças não é nulo como antes, agora ele é:
E essa é a força normal no caso sob aceleração.
Passo 3
Agora falta calcular o módulo e o ângulo necessários para produzir a aceleração .
Vamos começar aplicando a segunda lei de Newton na direção horizontal:
E a única força que age nessa direção é justamente a componente da força , então:
E agora, aplicando a segunda lei de Newton na direção vertical, encontramos o seguinte:
Onde , pois estamos considerando o caso sob aceleração:
Passo 4
Então temos os seguinte valores:
E já podemos calcular o módulo da força :
E também o ângulo que a força forma com a horizontal, conforme a figura:
Resposta
O módulo da força é , e forma um ângulo de com a horizontal. A força normal no caso estático é , e no caso sob aceleração é .