Vigas Compostas
Teoria
Introdução
Um belo dia, munido com seus conhecimentos de resistência dos materiais, você decide reformar os móveis da sua casa.
Você encontra um banco de madeira que deve resistir a um certo momento fletor e decide reforça-lo com uma placa de aço:
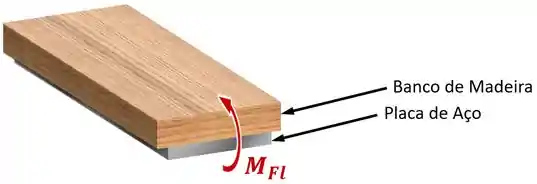
Ao fazer isso, você criou uma viga composta por dois materiais.
E aí aqui surge uma dúvida:
Como que vão ficar as tensões em cada material devido ao momento fletor aplicado nessa viga composta?
Método da Seção Transformada
Para descobrir como vão ficar essas tensões , o caminho é usar o método da seção transformada.
Esse método consiste em transformar a seção transversal composta pelos dois materiais em uma seção equivalente feita de um único material.
Podemos, por exemplo, pegar a parte da seção que é de madeira e transformá-la em uma parte equivalente de aço. (Ou vice-versa!)
E como fazemos essa transformação?
Fazemos ela definindo um fator de transformação , que é uma razão entre o módulo de elasticidade da parte que está sendo “transformada” e o módulo de elasticidade parte que vai permanecer intacta:
Escolhendo transformar, por exemplo, a parte de madeira em uma parte equivalente de aço, teríamos que:
Nesse caso, como o aço tem um módulo de elasticidade maior que a madeira, o fator será menor do que .
Mas caso a gente escolhesse por transformar aço em madeira, teríamos o inverso e seria maior do que .
Definido esse fator, nós devemos identificar a largura original da parte que será transformada, para, em seguida, calcularmos a nova largura dessa parte:
Assim, completamos a transformação da seção antiga composta em uma seção equivalente/transformada feita de um único material:
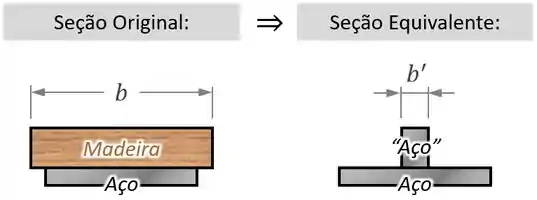
Cálculo das Propriedades Geométricas
Depois que a seção equivalente tiver sido definida, nós podemos calcular normalmente para ela:
- A posição da sua linha neutra;
- & e o seu momento de inércia da área (ou só “” para alguns professores),
Usando os métodos que vimos lá quando estudamos a fórmula da flexão, resumidos na figura abaixo:
Lembrando que o momento de inércia da área de um elemento é dado pela fórmula para elementos retangulares e para elementos circulares.
Cálculo das Tensões nos Materiais
Calculadas as propriedades geométricas para a seção equivalente, vamos estar prontos para descrever as tensões nos materiais.
Como?
Usando a fórmula da flexão, mas com uma diferença MUITO IMPORTANTE!
Para o cálculo das tensões nas partes que ficaram intactas, vamos usar a fórmula da flexão de sempre:
...que para alguns professores é escrita como só .
Mas para o cálculo das tensões nas partes que foram transformadas, vamos multiplicar a fórmula da flexão pelo fator de transformação :
Como no exemplo abaixo:
Distribuição de tensões
Por fim, alguns exercícios podem pedir que você desenhe a distribuição das tensões de flexão em uma seção transversal de uma viga composta.
Nesse caso, você deve não só calcular as tensões máximas em cada material, como também calcular as tensões em cada material no ponto de junção entre os materiais.
Aí, marcando as tensões calculadas em um gráfico posição tensão e ligando os pontos por retas, vamos ter a distribuição de tensões na seção da viga composta, como mostra a imagem abaixo:
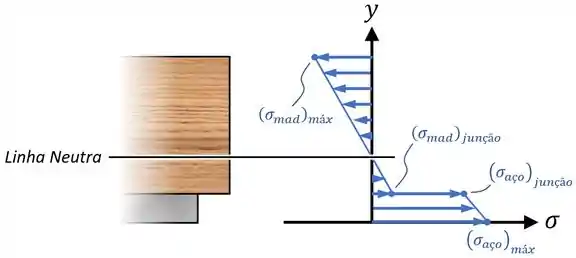
Sendo que nesse gráfico, dá para observar como sempre vai haver um salto (aumento OU redução) de tensão nos pontos de junção entre materiais.
Método da Seção Transformada
Cálculo das Propriedades Geométricas
Cálculo das Tensões nos Materiais
Distribuição de tensões
Exercícios Resolvidos
Exercício Resolvido #1
Russell Charles Hibbeler, Resistência dos Materiais, 7ª ed. São Paulo: Pearson Prentice Hall, 2010, pp. 239&240-6.125.
A viga composta é feita de aço A-36 e latão vermelho C83400 e tem a seção transversal mostrada na figura. Se for submetida a um momento , determine a tensão máxima no latão e no aço. Determine também a tensão em cada material na junção entre eles.
Dados: , .
Passo 1
O que está acontecendo?
Nesse exercício, nós temos uma viga composta por uma parte superior de aço (com módulo de elasticidade ) e uma parte inferior de latão (com módulo de elasticidade ).
Além disso, tanto a parte de aço quanto a parte de latão possuem uma altura e uma largura ou base .
A viga é submetida a um momento , que vai gerar tensões normais de flexão nela.
Mas como ela é composta, não podemos usar diretamente a fórmula da flexão nela.
Precisamos primeiro usar o método da seção transformada (que também pode ter infinitos outros nomes como método da área equivalente ou método da largura equivalente).
De acordo com esse método, se escolhermos transformar a parte de latão em uma parte equivalente de aço, por exemplo, devemos definir um fator de transformação :
Para depois calcular a largura da parte de aço equivalente à parte de latão:
Dessa forma, vamos conseguir definir uma seção transformada ou equivalente feita toda de aço:
Assim, para essa seção transformada, será possível calcular as tensões normais de flexão normalmente, através dos passos que já conhecemos:
- Determinação da posição da linha neutra;
- Determinação do momento de inércia da área para a seção;
- E finalmente, aplicação da fórmula da flexão .
Aí, ao final, as tensões no aço podem ser calculadas diretamente pela fórmula da flexão, enquanto que as tensões no latão, que teve sua largura transformada, devem ser multiplicadas por .
Ou seja:
E o que é que o exercício quer?
Ele quer saber a tensão máxima no latão e no aço, que vão ocorrer nas bordas inferior e superior da seção.
Além disso, ele também que a gente determine as tensões no latão e no aço no ponto em que há a interface entre esses materiais.
Então, para resolver o exercício, vamos:
- Transformar a seção composta em uma seção transformada feita toda de aço;
- Calcular as propriedades geométricas ( e ) para essa seção transformada;
- Identificar as posições em relação à linha neutra das bordas inferior e superior da seção, além da posição da borda entre os materiais;
- E, finalmente, aplicar a fórmula para determinar as tensões no aço e a fórmula para determinar as tensões no latão, uma vez que o latão teve sua largura transformada anteriormente.
Passo 2
Então vamos lá!
Primeiro, vamos fazer a:
Para tanto, começamos definindo o fator de transformação:
Substituindo os valores desses módulos de elasticidade de acordo com os dados fornecidos pelo exercício, vamos ter que:
Agora, podemos calcular o valor da largura da parte de aço equivalente à parte de latão:
Substituindo e a largura original da parte de latão, , temos:
Dessa forma, a nossa seção transformada fica assim:
Passo 3
Agora, podemos determinas as:
Primeiro, determinamos a posição da linha neutra.
Para tanto, começamos numerando os elementos da seção transformada e estabelecendo a base da seção como a posição :
Com isso, podemos preencher uma tabela com os valores das áreas e das posições dos centros de cada elemento:
Sendo que, ainda nessa tabela, também preenchemos na coluna final os valores dos produtos para cada elemento e na linha final os valores dos somatórios das áreas e dos produtos .
Assim, podemos finalmente calcular a posição da linha neutra:
Passo 4
Depois de termos calculado a posição da linha neutra, calculamos o momento de inércia da área para a seção transformada.
Começamos calculando o momento de inércia da área de cada elemento.
Para o elemento retangular , vamos ter:
Já para o elemento retangular , que tem a base transformada , vamos ter:
Em seguida, temos que determinar as distâncias entre o centro de cada elemento e a linha neutra:
O centro do elemento está a uma altura de , então sua distância vai ser:
Já o centro do elemento está a uma altura de , então sua distância vai ser:
Com isso, podemos agora aplicar a fórmula abaixo, baseada no teorema dos eixos paralelos, para determinar o momento de inércia da área da seção transformada como um todo:
Realizando esse somatório, temos:
Substituindo os valores:
- , e ;
- & , e ,
E calculando tudo, vamos encontrar que:
Passo 5
Finalmente, podemos fazer o:
Aqui, devemos primeiro identificar as posições em relação à linha neutra dos pontos em que queremos calcular as tensões no aço e no latão.
Como queremos calcular as tensões nas bordas inferior e superior da seção, e na borda entre os materiais, vamos observar as posições dessas bordas:
Desse esquema acima, vemos que a borda superior tem uma posição em relação à linha neutra:
Já a borda na junção entre os materiais tem uma posição:
Enquanto que a borda inferior tem uma posição:
Dessa forma, a tensão na borda superior, que vai ser a tensão máxima na região superior ocupada pelo aço, vai ser:
Substituindo todos os valores em função de e :
- ;
- ;
- & ,
- ;
- ;
- e ;
- & ,
Encontramos que:
Simplificando isso, e sabendo que é o mesmo que , temos que:
O que dá:
Já a tensão no aço na região da junção entre os materiais vai ser:
Seguindo os mesmos passos da tensão que acabamos de calcular, mas dessa vez usando , vemos encontrar que:
O que dá:
Agora...
Para as tensões no latão, que teve sua largura transformada pelo fator de transformação , a fórmula da flexão deve ser multiplicada por .
Dessa forma, a tensão na borda inferior, que vai ser a tensão máxima na região inferior ocupada pelo latão, vai ser:
Enquanto que a tensão no latão na região da junção entre os materiais vai ser:
Substituindo nessas equações todos os valores em função de e :
Elas ficam assim:
Daí, calculando tudo e sabendo que é o mesmo que , encontramos que:
E assim terminamos o nosso exercício!
Por fim, na hora de fornecer os resultados, podemos colocar somente os seus valores absolutos e indicar entre parênteses se são tensões de tração ou compressão:
Resposta
Exercício Resolvido #2
Russell Charles Hibbeler, Resistência dos Materiais, 7ª ed. São Paulo: Pearson Prentice Hall, 2010, pp. 239-6.121.
As partes superior e inferior da viga de madeira são reforçadas com tiras de aço, como mostra a figura. Determine a tensão de flexão máxima desenvolvida na madeira e no aço se a viga for submetida a um momento fletor . Trace um rascunho da distribuição de tensão que age na seção transversal. Considere , .
Passo 1
O que está acontecendo?
A viga é composta por:
- Uma seção central de madeira de base e altura , com um módulo de elasticidade ;
- E tiras de aço nas partes superior e inferior, com bases , alturas e um módulo de elasticidade .
Ela é submetida a um momento , que vai gerar tensões normais de flexão nela.
Mas como ela é composta, não podemos usar diretamente a fórmula da flexão nela.
Precisamos primeiro usar o método da seção transformada.
E o que é que o exercício quer?
Ele quer saber as tensões de flexão máximas na madeira e no aço devido ao momento aplicado.
Além disso, ele ainda quer que a gente faça um rascunho da distribuição de tensões que age na seção transversal dessa viga.
Então, para resolver esse exercício, vamos ter que:
1. Transformar a seção composta em uma seção transformada feita toda de um material;
Aqui, escolhendo por transformar a parte de madeira em uma parte equivalente de aço, vamos ter que definir um fator de transformação e calcular a largura da parte equivalente.
2. Calcular as propriedades geométricas ( e ) para essa seção transformada;
Aqui, como essa viga é simétrica em relação à horizontal, já conseguimos perceber que a sua linha neutra vai estar na posição central .
& 3. Calcular as tensões na madeira e no aço usando a fórmula da flexão, sabendo que as tensões na madeira devem ser multiplicadas por , uma vez que ela teve sua largura transformada.
Ou seja, vamos calcular as tensões no aço através da fórmula:
E as tensões na madeira através da fórmula:
Passo 2
Então vamos começar pelo primeiro passo, que é a:
Para tanto, definimos o fator de transformação:
E calculamos o valor da largura da parte de aço equivalente à parte de madeira:
Substituindo e a largura original da parte de madeira, , temos:
Dessa forma, a nossa seção transformada, com a linha neutra já no meio (uma vez que essa seção é simétrica em relação à horizontal), fica assim:
Passo 3
Agora, vamos seguir com o cálculo das:
Como vimos no passo e já representamos na figura ao final do passo anterior, já sabemos a posição da linha neutra para essa viga, que é simétrica em relação á horizontal.
Então aqui, só precisamos calcular o momento de inércia da área para a seção transformada.
Começamos numerando os elementos da seção:
Em seguida, aproveitando a imagem acima, calculamos, para cada elemento, o momento de inércia da área , a área e a distância entre o centro do elemento e a linha neutra.
Para os elemento retangulares e , vamos ter um momento de inércia da área:
Uma área:
E por fim, tendo em mente:
- Que o centro do elemento está a uma altura de ;
- E que o centro do elemento está a uma altura de ,
...vamos ter distâncias entre os seus centros e a linha neutra de altura :
Já para o elemento retangular central , vamos ter que:
E que:
Além disso, tendo em mente que o centro do elemento está localizado na linha neutra, vamos ter uma distância em relação à linha neutra:
Com isso, podemos agora aplicar a fórmula abaixo, baseada no teorema dos eixos paralelos, para determinar o momento de inércia da área da seção transformada como um todo:
Realizando esse somatório, temos:
Aí aqui, como os elementos e tem momentos de inércia da área idênticos, áreas idênticas e distâncias idênticas, podemos simplificar essa equação, deixando ela assim:
Substituindo os valores:
- , e ;
- & , e ,
E calculando tudo, encontramos que:
Passo 4
Finalmente, podemos fazer o:
Aqui, podemos observar a geometria da nossa seção:
E perceber que:
- Os valores máximos positivo e negativo da posição relativa à linha neutra para as partes de aço (elementos e ) vão ser ;
- Enquanto que os valores máximos positivo e negativo dessa posição para a parte de madeira (elemento ) vai ser .
Então, aplicando a fórmula da flexão para o aço, vamos ter:
Substituindo, para o aço:
- ;
- Os valores máximos positivo e negativo de ;
- & ,
- ;
- ;
- Os valores máximos positivo e negativo de para a parte de madeira, ;
- & ,
- Que a tensão normal de flexão sempre varia linearmente com a variação da posição em uma seção transversal, como mostram as fórmulas e ;
- Que a tensão na madeira varia de no topo da parte de madeira até na base, passando por uma tensão nula na linha neutra da seção;
- E que a tensão no aço é de no topo da viga e de na base da viga.
- ;
- Os valores de nos pontos em que o aço se encontra com a madeira, ;
- & ,
Vamos ter que as tensões máximas no aço vão ser:
Calculando tudo e sabendo que é o mesmo que , encontramos que:
Sendo que o valor negativo (de compressão) ocorre para o topo da seção, onde , e o valor positivo (de tração) ocorre para a base da seção, onde .
Em seguida, aplicamos a fórmula da flexão para a madeira, que fica multiplicada pelo fator de transformação , uma vez que a madeira teve a sua largura transformada:
Substituindo:
Vamos encontrar as tensões máximas na madeira:
Calculando tudo e sabendo que é o mesmo que , encontramos que:
Sendo que o valor negativo (de compressão) ocorre para o topo da parte de madeira, onde , e o valor positivo (de tração) ocorre para a base da parte de madeira, onde .
Passo 6
Por fim, o exercício ainda quer que a gente faça um esboço da distribuição de tensões nessa seção transversal, então vamos lá!
Sabemos:
Assim, para conseguirmos desenhar a distribuição de tensões na seção transversal, só falta conhecermos a tensão no aço nos pontos em que ele se encontra com a madeira ().
Aplicando a fórmula da flexão de novo para o aço, temos:
Substituindo:
Vamos ter que as tensões no aço nesses pontos de encontro com a madeira vão ser:
O que dá:
Sendo que o valor negativo (de compressão) ocorre no ponto de encontro da tira superior com a madeira, onde , e o valor positivo (de tração) ocorre no encontro da tira inferior com a madeira, onde .
Dessa forma, o nosso rascunho da distribuição de tensões na seção transversal dessa viga fica assim:
Normalmente, é necessário definir eixos e nesses rascunhos.
Definindo um eixo iniciando na base da viga, o rascunho fica assim:
E pronto, traçamos o rascunho pedido pelo exercício!
Na hora de definir a resposta final do exercício, podemos indicar somente os valores absolutos das tensões máximas no aço e na madeira, e assim terminamos nosso exercício:
Resposta
Exercício Resolvido #3
Ferdinand P. Beer et al., Mecânica dos materiais, 5ª ed. Porto Alegre: AMGH, 2011, pp. 259-4.40.
Uma barra de aço () e uma barra de alumínio () são unidas para formar a barra composta mostrada na figura. Determine a tensão máxima, no alumínio e no aço, quando a barra é flexionada em torno do eixo horizontal, com .
Passo 1
O que está acontecendo?
A viga composta da figura é feita de aço (com um módulo de elasticidade ) e alumínio (com um módulo de elasticidade ).
Um momento em torno do eixo horizontal é aplicado nessa viga, gerando tensões normais de flexão nela.
Lembrando que, como a viga é composta, precisamos usar o método da seção transformada para calcular essas tensões nela.
E o que é que o exercício quer?
Ele quer saber as tensões máximas no alumínio e no aço nessa viga.
Para tanto, vamos ter que:
1. Transformar a seção composta em uma seção transformada feita toda de um material;
Aqui, escolhendo por transformar a parte de aço em uma parte equivalente de alumínio, vamos ter que definir um fator de transformação para podermos calcular a largura da parte equivalente.
2. Calcular as propriedades geométricas ( e ) para essa seção transformada;
& 3. Calcular as tensões no alumínio e no aço usando a fórmula da flexão, sabendo que as tensões no aço devem ser multiplicadas por , uma vez que ele teve sua largura transformada.
Ou seja, vamos calcular as tensões no alumínio através da fórmula:
E as tensões no aço através da fórmula:
Passo 2
Então vamos começar pelo primeiro passo, que é a:
Começamos definindo o fator de transformação:
E calculamos o valor da largura da parte de alumínio equivalente à parte de aço:
Aqui, substituindo e vendo na figura do exercício que a parte de aço tem uma largura original , vamos ter que:
Dessa forma, a nossa seção transformada fica assim:
Passo 3
Agora, vamos seguir com o cálculo das:
Primeiro, devemos encontrar a posição da linha neutra para essa seção transformada.
Então vamos lá!
Começamos separando a nossa seção transformada em elementos numerados e definimos a base da seção como a posição :
Feito isso, preenchemos em uma tabela os valores das áreas e das posições dos centros de cada elemento, aproveitando as dimensões do desenho feito ao final do passo anterior:
Nessa tabela, ainda preenchemos na última coluna o valor do produto para cada elemento e na última linha o valor dos somatórios das áreas e dos produtos .
Assim, conseguimos calcular a posição da linha neutra:
Passo 4
Calculada a posição da linha neutra, podemos agora calcular o momento de inércia da área para a seção transformada.
Para tanto, começamos calculando o momento de inércia da área de cada elemento, aproveitando as dimensões de cada elemento indicadas nos desenhos anteriores.
Para o elemento , que é retangular de base e altura , vamos ter:
Já para o elemento , retangular de base e altura , temos:
Em seguida, temos que determinar as distâncias entre o centro de cada elemento e a linha neutra:
O centro do elemento está a uma altura de , então sua distância vai dar:
Já o centro do elemento está a uma altura de , então sua distância vai dar:
Com isso, podemos agora aplicar a fórmula abaixo, baseada no teorema dos eixos paralelos, para determinar o momento de inércia da área da seção transformada como um todo:
Realizando esse somatório, temos:
Substituindo os valores:
- , e ;
- & , e ,
E calculando tudo, vamos encontrar que:
Passo 5
Finalmente, podemos fazer o:
Aqui, devemos primeiro identificar as posições em relação à linha neutra dos pontos em que queremos calcular as tensões no alumínio e no aço.
Queremos calcular as tensões máximas no alumínio e no aço, então queremos usar as posições máximas em termos absolutos para o alumínio e para o aço.
Olhando para os desenhos anteriores que fizemos para a nossa seção, vemos que:
- Os pontos do alumínio mais distantes da linha neutra ficam na borda inferior da viga, onde ;
- Enquanto que os pontos do aço mais distantes da linha neutra ficam na borda superior da viga, onde .
Então, aplicando a fórmula da flexão para o cálculo da tensão máxima no alumínio, vamos ter:
Substituindo os valores abaixo, sempre em função das unidades e :
- ;
- ;
- & ,
- ;
- ;
- ;
- & ,
Vamos ter que:
Calculando isso e sabendo que é o mesmo que , encontramos que:
O que é uma tensão de tração, como demonstrado pelo sinal positivo.
Já para o aço, como ele teve sua largura transformada por um fator de transformação , a sua fórmula da flexão deve ser multiplicada por .
Dessa fórmula, aplicando a fórmula da flexão, multiplicada por , para o cálculo da tensão máxima no aço, vamos ter:
Aí, substituindo os valores, sempre em função de e :
E calculando tudo, vamos encontrar que:
O que é uma tensão de compressão, como demonstrado pelo sinal negativo.
E assim, lembrando que a letra queria saber a tensão máxima no alumínio e a letra queria saber a tensão máxima no aço, terminamos o nosso exercício:
Resposta
Exercício Resolvido #4
Elaboração própria
A viga de madeira abaixo foi reforçada com duas hastes de aço como mostrado na figura. Sabendo que a seção aqui mostrada sofre a ação de um esforço de flexão de modulo 127KN.m determine o valor da tensão normal que aparece na extremidade das barras de aço e na interface Aço-madeira. Usar e . Atenção ao eixo utilizado.
Passo 1
Para resolvermos esse tipo de questão, temos que ter na mente duas situações muito importante. A primeira é saber que algum dos materiais terá que ser transformado em um equivalente do outro. E que para fazer essa equivalência precisamos calcular o valor de n e b’.
Executado esses dois primeiros passos, todo o resto se torna mais fácil pois usamos as fórmulas de flexão que já conhecemos.
Então vamos lá, sabemos que o cálculo de n depende dos materiais que serão transformados e dos módulos de elasticidade.
A fórmula é
Por conveniência eu sempre escolho transformar o material de módulo de elasticidade menor, nesse caso a madeira, dessa forma o nosso valor de n será
Para determinar b’ é simples, é só multiplicar a largura do material que iremos transformar pelo valor de n que determinamos antes, então
Agora é como se tivéssemos uma seção retangular inteira de aço, em que o próximo passo será determinar o valor das tensões.
Passo 2
Agora que já sabemos como é nossa seção equivalente, devemos saber algumas coisas sobre como iremos calcular as nossas tensões normais
Primeiro temos que saber que a fórmula entre as tensões na parte intacta e na parte transformada são calculadas por fórmulas diferentes, e as fórmulas são
Ou seja, na parte transformada consideramos para o cálculo da tensão o valor de n.
Outro ponto importante é se atentar para o valor de Y quando for calcular tanto a seção intacta quanto a transformada. Agora que já sabemos isso vamos ao cálculo.
Passo 3
Sabemos que o valor do momento é facilmente adquirido, além do mais ele já foi dado no enunciado
Com relação ao valor de Y teremos que
Lembrando que o negativo existe pelo fato de arbitrarmos y negativo pra cima
Também já calculamos no primeiro passo o valor de n, logo
Agora só falta o momento de inércia
Passo 4
Aqui tem que tomar cuidado, pois o momento de inercia é feito para seção transformada e valerá o mesmo tanto para o trecho intacto quanto para o trecho transformado.
A nossa seção equivalente é
Como se trata de uma seção retangular teremos que fazer
Substituindo teremos que
Passo 5
Agora que já temos todos os valores basta calcularmos as tensões
Para o caso intacto, temos o ponto extremo do aço e o ponto interface aço madeira, então calcularemos duas tensões.
Caso extremidade do aço
Caso interface aço-madeira
Passo 6
Caso interface madeira aço (caso transformado)
Substituindo
Resposta
extremidade do aço
interface aço-madeira
Caso interface madeira aço (caso transformado)
Exercício Resolvido #5
Elaboração própria
uma peça de madeira foi reforçada com uma barra de ferro como mostras a figura. Usando seus conhecimentos sobre vigas compostas e sabendo que o modulo de elasticidade da madeira é dado por e determine a tensão na extremidade do aço e na interface aço madeira. O momento fletor que age sobe essa peça é de 15KN.m. observe os eixos usados.
Passo 1
Para resolvermos esse tipo de questão, temos que ter na mente duas situações muito importante. A primeira é saber que algum dos materiais terá que ser transformado em um equivalente do outro. E que para fazer essa equivalência precisamos calcular o valor de n e b’.
Executado esses dois primeiros passos, todo o resto se torna mais fácil pois usamos as fórmulas de flexão que já conhecemos.
Então vamos lá, sabemos que o cálculo de n depende dos materiais que serão transformados e dos módulos de elasticidade.
A fórmula é
Por conveniência eu sempre escolho transformar o material de módulo de elasticidade menor, nesse caso a madeira, dessa forma o nosso valor de n será
Para determinar b’ é simples, é só multiplicar a largura do material que iremos transformar pelo valor de n que determinamos antes, então
Agora temos um perfil T para resolvermos
Passo 2
Agora que já sabemos como é nossa seção equivalente, devemos saber algumas coisas sobre como iremos calcular as nossas tensões normais
Primeiro temos que saber que a fórmula entre as tensões na parte intacta e na parte transformada são calculadas por fórmulas diferentes, e as fórmulas são
Ou seja, na parte transformada consideramos para o cálculo da tensão o valor de n.
Outro ponto importante é se atentar para o valor de Y quando for calcular tanto a seção intacta quanto a transformada. Agora que já sabemos isso vamos ao cálculo.
Passo 3
Sabemos que o valor do momento é facilmente adquirido, além do mais ele já foi dado no enunciado
Com relação ao valor de Y teremos que descobrir a posição da linha neutra, para isso teremos que fazer o nosso passo a passo
Primeiro determinamos a origem do nosso sistema
Em seguida descobrimos quanto vale a área e a distância do centroide de cada elemento até a nossa origem.
Dessa forma descobrimos facilmente que
Definimos assim a nossa linha neutra
Com relação ao valor de Y teremos que
Para o trecho acima da linha neutra
Lembrando que o negativo existe pelo fato de arbitrarmos y negativo pra cima
Para o trecho abaixo da linha neutra
Também já calculamos no primeiro passo o valor de n, logo
Agora só falta o momento de inércia
Passo 4
Para o cálculo do momento de inércia teremos que usar de novo o nosso passo a passo. Sabemos que para calcularmos momentos de inercia precisamos determinar 3 coisas. As áreas de cada elemento, a distância do centroide de cada elemento até a linha neutra e por fim o momento de inercia de cada elemento. Como os elementos são retangulares, teremos que o momento de inercia deles é
A figura abaixo representa as distâncias dos centroides de cada elemento até a linha neutra
E nessa imagem temos as medidas para calcularmos os momentos de inercia
Calculando o momento de inercia de cada elemento teremos que
E no passo anterior já tínhamos determinado o valor das áreas
Agora que já temos todos os valores, bata calcularmos o momento de inercia para a fórmula
Passo 5
Agora que já temos todos os valores basta calcularmos as tensões
Para o caso intacto, temos o ponto extremo do aço e o ponto interface aço madeira, então calcularemos duas tensões.
Caso extremidade do aço
Caso interface aço-madeira
Passo 6
Caso interface madeira aço (caso transformado)
Substituindo
Caso madeira extremo
Substituindo
Resposta
extremidade do aço
interface aço-madeira
Caso interface madeira aço (caso transformado)
Caso madeira extremidade
Exercício Resolvido #6
Elaboração própria
Projetou-se uma passarela com seção transversal como o mostrado na figura. Sabendo que nessa seção da passarela existe a ação de um momento fletor de intensidade 235 KN.m determine o valor da tensão normal na extremidade do latão, na junção latão aço, na junção aço alumínio e na extremidade do alumínio. Atente-se ao sinal arbitrado.
Passo 1
Para resolvermos esse tipo de questão, temos que ter na mente duas situações muito importante. A primeira é saber que algum dos materiais terá que ser transformado em um equivalente do outro. E que para fazer essa equivalência precisamos calcular o valor de n e b’.
Executado esses dois primeiros passos, todo o resto se torna mais fácil pois usamos as fórmulas de flexão que já conhecemos.
Então vamos lá, sabemos que o cálculo de n depende dos materiais que serão transformados e dos módulos de elasticidade.
A fórmula é
Por conveniência eu sempre escolho transformar o material de módulo de elasticidade menor, nesse caso o latão e o alumínio, dessa forma o nosso valor de n será
Para determinar b’ é simples, é só multiplicar a largura do material que iremos transformar pelo valor de n que determinamos antes, então
Agora é como se tivéssemos uma seção retangular inteira de aço, em que o próximo passo será determinar o valor das tensões.
Passo 2
Agora que já sabemos como é nossa seção equivalente, devemos saber algumas coisas sobre como iremos calcular as nossas tensões normais
Primeiro temos que saber que a fórmula entre as tensões na parte intacta e na parte transformada são calculadas por fórmulas diferentes, e as fórmulas são
Ou seja, na parte transformada consideramos para o cálculo da tensão o valor de n.
Outro ponto importante é se atentar para o valor de Y quando for calcular tanto a seção intacta quanto a transformada. Agora que já sabemos isso vamos ao cálculo.
Passo 3
Sabemos que o valor do momento é facilmente adquirido, além do mais ele já foi dado no enunciado
Com relação ao valor de Y teremos que
Para o trecho acima da linha neutra
Lembrando que o negativo existe pelo fato de arbitrarmos y negativo pra cima
Para o trecho abaixo da linha neutra
Também já calculamos no primeiro passo o valor de n, logo
Agora só falta o momento de inércia
Passo 4
Aqui tem que tomar cuidado, pois o momento de inercia é feito para seção transformada e valerá o mesmo tanto para o trecho intacto quanto para o trecho transformado.
A nossa seção equivalente é
Como se trata de uma seção retangular teremos que fazer
Substituindo teremos que
Passo 5
Agora que já temos todos os valores basta calcularmos as tensões
Para o caso intacto, termos o ponto alumínio-aço e o ponto latão-aço, então calcularemos duas tensões.
Caso interface alumínio-aço
Caso interface latão-aço
Passo 6
Caso transformado
Caso interface alumínio-aço
Caso interface latão-aço
Caso alumínio-extremidade
Caso latão-extremidade
Resposta
Caso interface alumínio-aço
Caso interface latão-aço
Caso interface alumínio-aço
Caso interface latão-aço
Caso alumínio-extremidade
Caso latão-extremidade
Exercício Resolvido #7
Elaboração própria
Deseja-se projetar uma viga composta como a da figura para apoiar uma estrutura de aço. Com base em seus conhecimentos determine as tensões que aparecem na extremidade do aço, na junção aço latão, e na extremidade do latão. Atenção ao eixo usado.
Passo 1
Para resolvermos esse tipo de questão, temos que ter na mente duas situações muito importante. A primeira é saber que algum dos materiais terá que ser transformado em um equivalente do outro. E que para fazer essa equivalência precisamos calcular o valor de n e b’.
Executado esses dois primeiros passos, todo o resto se torna mais fácil pois usamos as fórmulas de flexão que já conhecemos.
Então vamos lá, sabemos que o cálculo de n depende dos materiais que serão transformados e dos módulos de elasticidade.
A fórmula é
Por conveniência eu sempre escolho transformar o material de módulo de elasticidade menor, nesse caso o latão, dessa forma o nosso valor de n será
Para determinar b’ é simples, é só multiplicar a largura do material que iremos transformar pelo valor de n que determinamos antes, então
Agora é como se tivéssemos uma seção retangular inteira de aço, em que o próximo passo será determinar o valor das tensões.
Passo 2
Agora que já sabemos como é nossa seção equivalente, devemos saber algumas coisas sobre como iremos calcular as nossas tensões normais
Primeiro temos que saber que a fórmula entre as tensões na parte intacta e na parte transformada são calculadas por fórmulas diferentes, e as fórmulas são
Ou seja, na parte transformada consideramos para o cálculo da tensão o valor de n.
Outro ponto importante é se atentar para o valor de Y quando for calcular tanto a seção intacta quanto a transformada. Agora que já sabemos isso vamos ao cálculo.
Passo 3
Sabemos que o valor do momento é facilmente adquirido, além do mais ele já foi dado no enunciado
Com relação ao valor de Y teremos que
Para o trecho acima da linha neutra
Lembrando que o negativo existe pelo fato de arbitrarmos y negativo pra cima
Para o trecho abaixo da linha neutra
Também já calculamos no primeiro passo o valor de n, logo
Agora só falta o momento de inércia
Passo 4
Aqui tem que tomar cuidado, pois o momento de inercia é feito para seção transformada e valerá o mesmo tanto para o trecho intacto quanto para o trecho transformado.
A nossa seção equivalente é
Como se trata de uma seção retangular teremos que fazer
Substituindo teremos que
Passo 5
Agora que já temos todos os valores basta calcularmos as tensões
Para o caso intacto, termos o ponto extremo do aço e o ponto interface aço madeira, então calcularemos duas tensões.
Caso extremidade do aço
Caso interface aço-latão
Passo 6
Caso interface latão-aço (caso transformado)
Substituindo
Caso extremidade latão
Substituindo
Resposta
Caso extremidade do aço
Caso interface aço-latão
Caso interface latão-aço (caso transformado)
Caso extremidade latão
Exercício Resolvido #8
Elaboração própria
Calcule o valor da tensão normal no ponto A indicado da viga composta.
Passo 1
Para resolvermos esse tipo de questão, temos que ter na mente duas situações muito importante. A primeira é saber que algum dos materiais terá que ser transformado em um equivalente do outro. E que para fazer essa equivalência precisamos calcular o valor de n e b’.
Executado esses dois primeiros passos, todo o resto se torna mais fácil pois usamos as fórmulas de flexão que já conhecemos.
Então vamos lá, sabemos que o cálculo de n depende dos materiais que serão transformados e dos módulos de elasticidade.
A fórmula é
Por conveniência eu sempre escolho transformar o material de módulo de elasticidade menor, nesse caso a madeira, dessa forma o nosso valor de n será
Para determinar b’ é simples, é só multiplicar a largura do material que iremos transformar pelo valor de n que determinamos antes, então
Agora temos um perfil retangular para resolvermos
Passo 2
Agora que já sabemos como é nossa seção equivalente, devemos saber algumas coisas sobre como iremos calcular as nossas tensões normais
Primeiro temos que saber que a fórmula entre as tensões na parte intacta e na parte transformada são calculadas por fórmulas diferentes, e as fórmulas são
Ou seja, na parte transformada consideramos para o cálculo da tensão o valor de n.
Outro ponto importante é se atentar para o valor de Y quando for calcular tanto a seção intacta quanto a transformada. Agora que já sabemos isso vamos ao cálculo.
Passo 3
Sabemos que o valor do momento é facilmente adquirido, além do mais ele já foi dado no enunciado
Com relação ao valor de Y teremos que descobrir a posição da linha neutra, como a nossa seção é simétrica, sabemos que a linha neutra passa no centro da seção
Com relação ao valor de Y basta calcularmos a distância da LN até o nosso ponto
A, dessa forma teremos
Lembrando que o negativo existe pelo fato de arbitrarmos y negativo pra cima
Para o trecho abaixo da linha neutra, pela simetria, temos os mesmos valores de cima.
Também já calculamos no primeiro passo o valor de n, logo
Agora só falta o momento de inércia
Passo 4
Aqui tem que tomar cuidado, pois o momento de inercia é feito para seção transformada e valerá o mesmo tanto para o trecho intacto quanto para o trecho transformado.
A nossa seção equivalente é
Como se trata de uma seção retangular teremos que fazer
Substituindo teremos que
Passo 5
Agora que já temos todos os valores basta calcularmos as tensões, como o nosso ponto A está na seção que foi transformada (a madeira) precisamos usar a fórmula
Substituindo
Resposta
Exercício Resolvido #9
Elaboração própria
Um tubo de aço é responsável por fazer o transporte de petróleo e outros matérias líquidos em uma determinada região. Para reforça-lo foram usadas barras de alumínio como as mostradas na figura. Sabendo que essa seção foi submetida a um esforço fletor de módulo ,determine o valor da tensão máxima normal que ocorrerá na viga composta.
Passo 1
Para resolvermos esse tipo de questão, temos que ter na mente duas situações muito importante. A primeira é saber que algum dos materiais terá que ser transformado em um equivalente do outro. E que para fazer essa equivalência precisamos calcular o valor de n e b’.
Executado esses dois primeiros passos, todo o resto se torna mais fácil pois usamos as fórmulas de flexão que já conhecemos.
Então vamos lá, sabemos que o cálculo de n depende dos materiais que serão transformados e dos módulos de elasticidade.
A fórmula é
Por conveniência eu sempre escolho transformar o material de módulo de elasticidade menor, nesse caso o alumínio, dessa forma o nosso valor de n será
Para determinar b’ é simples, é só multiplicar a largura do material que iremos transformar pelo valor de n que determinamos antes, então
Agora temos um perfil retangular para resolvermos
Passo 2
Agora que já sabemos como é nossa seção equivalente, devemos saber algumas coisas sobre como iremos calcular as nossas tensões normais
Primeiro temos que saber que a fórmula entre as tensões na parte intacta e na parte transformada são calculadas por fórmulas diferentes, e as fórmulas são
Ou seja, na parte transformada consideramos para o cálculo da tensão o valor de n.
Outro ponto importante é se atentar para o valor de Y quando for calcular tanto a seção intacta quanto a transformada. Agora que já sabemos isso vamos ao cálculo.
Passo 3
Sabemos que o valor do momento é facilmente adquirido, além do mais ele já foi dado no enunciado
Com relação ao valor de Y teremos que descobrir a posição da linha neutra, como a nossa seção é simétrica, sabemos que a linha neutra passa no centro da seção
Com relação ao valor de Y teremos que
Para o trecho acima da linha neutra
Lembrando que o negativo existe pelo fato de arbitrarmos y negativo pra cima
Para o trecho abaixo da linha neutra, pela simetria, temos os mesmos valores de cima.
Também já calculamos no primeiro passo o valor de n, logo
Agora só falta o momento de inércia
Passo 4
Para o cálculo do momento de inercia precisamos fazer uma diferença entre a seção cheia e a seção vazada para podermos calcular o momento de inercia da nossa peça, com isso teremos que
Calculando
Por ser uma seção retangular teremos que
Calculando
Por ser uma seção retangular teremos que
Logo o momento de inercia da seção será
Passo 5
Agora que já temos todos os valores basta calcularmos as tensões
Para o caso intacto, temos o ponto extremo do aço e o ponto interface aço alumínio, então calcularemos duas tensões.
Caso extremidade do aço-alumínio
Passo 6
Caso interface alumínio- aço (caso transformado)
Substituindo
Caso alumínio extremidade
Substituindo
Olhando o gráfico teremos que o valor máximo ocorre nas interface aço-alumínio no lado da peça intacta, logo teremos que
Resposta
Exercício Resolvido #10
Elaboração própria
Deseja-se reforçar uma barra de latão usando duas barras de aço como mostradas na figura. Sabendo disso determine o valor da tensão normal máxima sofrida por essa peça que sofre a ação de um momento fletor de intensidade .
Passo 1
Para resolvermos esse tipo de questão, temos que ter na mente duas situações muito importante. A primeira é saber que algum dos materiais terá que ser transformado em um equivalente do outro. E que para fazer essa equivalência precisamos calcular o valor de n e b’.
Executado esses dois primeiros passos, todo o resto se torna mais fácil pois usamos as fórmulas de flexão que já conhecemos.
Então vamos lá, sabemos que o cálculo de n depende dos materiais que serão transformados e dos módulos de elasticidade.
A fórmula é
Por conveniência eu sempre escolho transformar o material de módulo de elasticidade menor, nesse caso o latão, dessa forma o nosso valor de n será
Para determinar b’ é simples, é só multiplicar a largura do material que iremos transformar pelo valor de n que determinamos antes, então
Agora temos um perfil I para resolvermos
Passo 2
Agora que já sabemos como é nossa seção equivalente, devemos saber algumas coisas sobre como iremos calcular as nossas tensões normais
Primeiro temos que saber que a fórmula entre as tensões na parte intacta e na parte transformada são calculadas por fórmulas diferentes, e as fórmulas são
Ou seja, na parte transformada consideramos para o cálculo da tensão o valor de n.
Outro ponto importante é se atentar para o valor de Y quando for calcular tanto a seção intacta quanto a transformada. Agora que já sabemos isso vamos ao cálculo.
Passo 3
Sabemos que o valor do momento é facilmente adquirido, além do mais ele já foi dado no enunciado
Com relação ao valor de Y teremos que descobrir a posição da linha neutra, como a nossa seção é simétrica, sabemos que a linha neutra passa no centro da seção
Com relação ao valor de Y teremos que
Para o trecho acima da linha neutra
Lembrando que o negativo existe pelo fato de arbitrarmos y negativo pra cima
Para o trecho abaixo da linha neutra, pela simetria, temos os mesmos valores de cima.
Também já calculamos no primeiro passo o valor de n, logo
Agora só falta o momento de inércia
Passo 4
Para o cálculo do momento de inércia teremos que usar de novo o nosso passo a passo. Sabemos que para calcularmos momentos de inercia precisamos determinar 3 coisas. As áreas de cada elemento, a distância do centroide de cada elemento até a linha neutra e por fim o momento de inercia de cada elemento. Como os elementos são retangulares, teremos que o momento de inercia deles é
A figura abaixo representa as distâncias dos centroides de cada elemento até a linha neutra
Lembrando que o elemento do meio já tem seu centroide em cima da linha Neutra, logo esse valor na nossa conta é zero.
E nessa imagem temos as medidas para calcularmos os momentos de inercia
Calculando o momento de inercia de cada elemento teremos que
E no passo anterior já temos também como determinado o valor das áreas
Agora que já temos todos os valores, basta calcularmos o momento de inercia para a fórmula
Passo 5
Agora que já temos todos os valores basta calcularmos as tensões
Para o caso intacto, temos o ponto extremo do aço e o ponto interface aço latão, então calcularemos duas tensões.
Caso extremidade do aço
Caso interface aço-madeira
Passo 6
Caso interface latão aço (caso transformado)
Substituindo
Olhando o gráfico teremos que o valor máximo ocorre nas extremidades, logo teremos que
