Enunciado
Mecânica e Resistência dos Materiais - Hibbeler - Estática- Ed: 14º - Capítulo 4.Problemas - Ex. 95
Se , e , determine a intensidade e os ângulos diretores coordenados do momento de binário resultante.
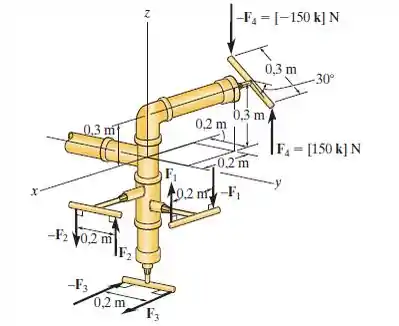
Passo 1
E aí Pessoal, tudo bem? Vamos dar início a mais uma questão juntos!
Precisamos determinar a intensidade do momento de binário resultante e o ângulo formado com os eixos coordenados.
A chave aqui é calcular separadamente os momentos dos 4 binários, cada um na forma vetorial, para só depois fazermos as somas e calcularmos o que a questão nos pede.
Lembrando, o momento de um binário é dado por:
Sendo a força, a distância perpendicular entre as forças e a direção do eixo.
Aah!! Não se esqueçam de utilizar a regra da mão direita para verificar se o momento é positivo ou negativo de acordo com o eixo analisado!
Passo 2
Agora que já sabemos o que devemos fazer, vamos para os cálculos! Vamos calcular os momentos de cada uma das forças. Começando pelo par , temos:
Para o binário formado pelas forças , temos:
Para ,
E por fim, para , temos:
Passo 3
Agora que já temos os 4 momentos na forma vetorial, podemos soma-los. Desta forma, temos o seguinte momento resultante:
E a sua intensidade é:
Passo 4
Para finalizarmos a questão, basta calcularmos os ângulos formados com os eixos coordenados. Eles são os ângulos , e formados com a direção positiva dos eixos , e , respectivamente.
Para calcularmos, temos:
E assim finalizamos a questão!