Enunciado
Mecânica e Resistência dos Materiais - Hibbeler - Estática- Ed: 14º - Capítulo 4.Problemas - Ex. 110
Substitua a força de que age sobre o encanamento por uma força e um momento de binário equivalentes no ponto .
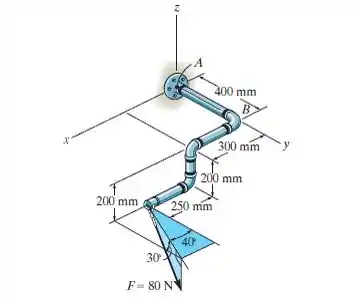
Passo 1
E aí Pessoal, tudo bem? Vamos dar início a mais uma questão juntos!
A ideia aqui é substituir a força dadas no enunciado da questão por uma força resultante e por um momento , ambos em relação ao ponto .
A parte da força é bastante simples. A força resultante é exatamente a força . A única coisa que devemos fazer aqui é escrever ela na forma vetorial.
Já em relação ao momento, vamos ter que calcular o momento devido a essa força em relação ao ponto . Para isto, posteriormente, iremos utilizar a notação vetorial para facilitar as contas!
Então, vamos aos cálculos!
Passo 2
A ideia para escrevermos a força na força vetorial é sair decompondo-a.
Primeiro, sabemos que a força forma um ângulo de 30° com o plano . Portanto, já podemos decompor ela em uma parte perpendicular ao plano (direção ) e outra contida no plano!
Desta forma, temos:
Ao decompormos as forças é bastante importante prestarmos atenção no sistema de coordenadas! Como o eixo é positivo “para cima”, e a força aponta “para baixo”, a componente deve ser negativa!
Agora, vamos decompor essa força em uma paralela ao eixo , , e uma paralela ao eixo , . Sabendo que forma um ângulo de com o eixo , temos:
Portanto, a força resultante é:
E assim finalizamos a primeira parte da questão!
Passo 3
Para finalizarmos, temos que calcular o momento em relação ao ponto
Calculando através da relação vetorial, temos:
E assim finalizamos a questão!
Resposta
A força resultante é
E o momento de binário é