Enunciado
Mecânica e Resistência dos Materiais - Hibbeler - Estática- Ed: 14º - Capítulo 4.Problemas - Ex. 120
Substitua o carregamento por uma única força resultante. Especifique onde sua linha de ação intercepta uma linha horizontal ao longo do membro , medindo a partir de .
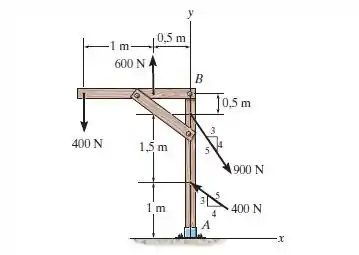
Passo 1
E aí Pessoal, tudo bem? Vamos dar início a mais uma questão juntos!
Mas, antes disto, precisamos fazer um breve comentário: quem é o ponto ??? A questão não especifica quem é exatamente este ponto. Logo, a questão é inconclusiva.
Entretanto, vamos “resolver” ela aqui. Para isto, vamos assumir que o ponto é o extremo do segmento horizontal que contém . Isto é, ele é exatamente o ponto de aplicação da força de .
Então, vamos dar continuidade a questão!
A questão nos pede para substituirmos todo o carregamento do desenho por uma única força resultante , com uma direção , que passa por um ponto a uma distância a direita do ponto . Percebam que iremos substituir por apenas uma força, com nenhum momento!
Então, a questão nos pede para determinarmos quem é a força , a direção e a distância .
Portanto, temos que trabalhar com duas frentes. Primeiro vamos trabalhar com o somatório das forças. Lembrando, a força resultante é:
Para nos auxiliar nesta etapa, vamos trabalhar com a notação vetorial, sendo a direção vertical e positiva para cima, e horizontal positiva para a direita.
Depois, para descobrirmos a distância , vamos trabalhar com o somatório dos momentos. Portanto,
Então, vamos aos cálculos!
Passo 2
Primeiramente, vamos determinar a força resultante.
Aqui vamos dividir em duas etapas: calcular a componente e depois a componente . Para calcularmos , devemos analisar quais forças possuem componente horizontal.
Nesta questão temos as forças de e . Portanto,
Já para a componente vertical, temos:
Portanto, a força resultante é:
Uma força de formando um ângulo medido no sentido horário com a direção positiva do eixo .
Passo 3
Para finalizarmos, temos que calcular o momento em relação ao ponto . Para facilitar a nossa vida, como as forças estão inclinadas, em relação aos eixos coordenados, vamos trabalhar aqui com a forma vetorial.
Portanto, vamos calcular os momentos vetorialmente e depois fazer a soma deles. Começando pela força (a inclinada aqui, a outra vertical a gente faz depois), temos:
Lembrem-se que o vetor é o vetor distância da origem até o ponto de aplicação da força .
Já para a força , temos:
E para a força ,
E por fim, para (agora sim a força vertical), temos:
Agora vamos calcular o momento devido a força resultante. Logo,
Portanto, o momento resultante é:
E assim finalizamos a questão!
Resposta
Uma força de formando um ângulo medido no sentido horário com a direção positiva do eixo . A distância é a direita do ponto .