Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Estática- Ed: 9º - Capítulo 8.Problemas - Ex. 102

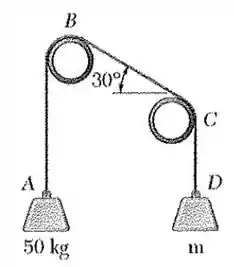
102. Uma corda A B C D está amarrada em dois canos, como mostra a figura. Sabendo que o coeficiente de atrito estático é 0,25 , determine (a) o menor valor da massa m para a qual o equilíbrio é possível, (b) a correspondente tração na parte B C da corda

Passo 1

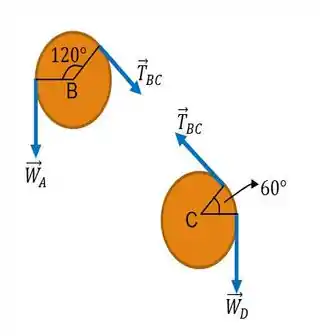
Bom! Antes de mais nada, a primeira coisa que temos que fazer é o esboço do nosso sisteminha, com as forças que nele estão atuando; o chamado diagrama de corpo livre.

E em seguida, vamos usar a seguinte equação para problemas que envolvem atritos em correia:

T 2 T 1 = e β μ s

Onde T 2 , é a maior tração, e T 1 , é a menor tração. Baseado nisso, temos que fazer uma análise separada para os canos B e C .

Passo 2

Vamos lá! Para o cano B , a maior força é W A e a menor força é T B C . Ficamos então, com a seguinte relação:

T 2 T 1 = e β μ s

W A T B C = e β μ s

Bom! O coeficeiente de atrito estático, μ s , nós já sabemos ser igual a 0,25 . E o ângulo β , da figura do P a s s o   1 , tiramos que vale 120 ° ou 2 π / 3   radianos. Obtemos, desse modo, a seguinte relação:

W A T B C = e 2 π 3 ⋅ 0,25

W A T B C = e π / 6  

Passo 3

Já para o cano C , a maior força é T B C e a menor força é W D . Ficamos então, com a seguinte relação:

T 2 T 1 = e β μ s

T B C W D = e β μ s

Bom! O coeficeiente de atrito estático, μ s , nós já sabemos ser igual a 0,25 . E o ângulo β , da figura do P a s s o   1 , tiramos que vale 60 ° ou π / 3   radianos. Obtemos, desse modo, a seguinte relação:

T B C W D = e π 3 ⋅ 0,25

T B C W D = e π / 12  

Passo 4

  1. E depois? O que fazemos com essas relações que obtivemos nos P a s s o s   2 e 3 ? Repara que o termo T B C está presente nas duas. O que acha de multiplicarmos as duas relações e ver se podemos tirar algo interessante? Vamos fazer isso:

T B C W D ⋅ W A T B C = e π / 6 ⋅ e π / 12  

W A W D = e π / 6 + π / 12

W A W D = e π / 4

W A W D = 2,193

W D = W A 2,193

E como a massa m A em B , que corresponde à W A é igual a 50   k g :

W D = 50   k g ⋅ g 2,193

m D g = 50   k g ⋅ g 2,193

m D = 50   k g ⋅ g 2,193 g

m D ≅ 22,8   k g

b) Para obter o valor de T B C , basta saber que:

W A T B C = e π / 6  

m A g T B C = e π / 6  

T B C = m A g e π / 6  

T B C = ( 50   k g ) ( 9,81   m / s 2 ) e π / 6  

T B C = 290,56   N

Resposta

a) m D ≅ 22,8   k g  

b)   T B C = 290,56   N ≅ 291   N

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Um carrinho de mão carregado é colocado em uma inclinação acidentada. O peso combinado do carrinho de mão e sua carga atua no centro de gravidade G. (a) Determine o ângulo máximo θ para o qual o carri
O corpo homogêneo com dois pés pequenos e duas rodas ideais estão em repouso na inclinação acidentada. (a) Suponha sem derrapagem e determine o valor máximo do ângulo θ para o qual o corpo não vira em
Um carpinteiro de 100k g se agacha sobre uma folha de 18k g de contraplacado quando ele está prestes a efetuar um conserto de telhas. Determine a força de atrito que a superfície do telhado exerce sob
Repita o Prob. 6 / 28 , mas agora o carro tem roda dianteira.
A força P é aplicada a (a) o bloco de 60l b e (b) o bloco de 100l b . Para cada caso, determine omagnitude de P necessária para iniciar o movimento.