102- Para a estrutura e carregamento mostrados na figura, determine os componentes de todas as forças atuantes no elemento .

Passo 1
Vamos começar analisando a força nas bases e analisando o corpo todo.

Se fizermos a somatória dos momentos em temos:
Sentido para cima.
Passo 2
Agora vamos começar a analisar a barra sabendo que a barra forma uma angulação com a horizontal igual a .
Pois o pino em tem o mesmo esquema de plano inclinado da questão anterior por ser um pino.
Agora desenhando as reações em temos:
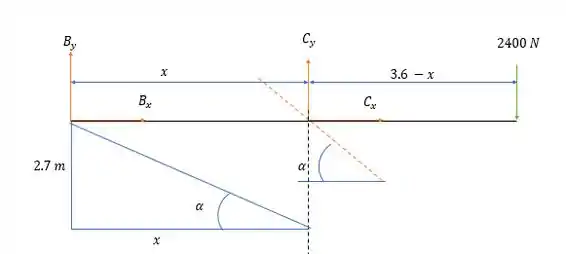
Onde a distância na figura vale:
E agora fazendo a somatória dos momentos em nós teremos:
Força essa que atua para baixo nessa barra e que apontará para cima na barra (por ação e reação).
Agora se fizermos a soma das forças verticais nós teremos:
Força que aponta para cima, agora calculando o valor de nós teremos que olhar para o seguinte plano inclinado.
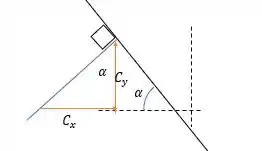
Onde:
Com isso pela soma das forças horizontais temos que:
Força essa que apontará para a esquerda nessa barra mas apontando para a direita em .
Passo 3
Agora vamos desenhar a barra de maior interesse que é .

Fazendo a somatória dos momentos em nós temos:
Força com sentido para a esquerda.
Agora para achar as forças em vamos fazer o somatório das forças.
Começando pelas forças verticais temos:
Força que aponta para baixo.
Agora a somatória das forças horizontais:
Força que aponta para a esquerda.