Determine a força em cada membro da treliça tesoura dupla em função da carga e indique se os membros estão sob tração ou compressão.
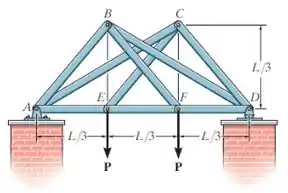
Passo 1
Vamos desenhar o diagrama de corpo lvre dessa treliça tesoura dupla!

Passo 2
Para todo corpo em equilíbrio, o somatório dos momentos em relação a um ponto deve ser igual a zero. Então, vamos calular o momentoem relação ao ponto . Adotando como sentido positivo o horário, temos:
Além dos momentos, o somatório das forças nos eixos de referência (, para um corpo em equilíbrio, deve ser igual a zero. Assim, adotando como referência positiva a direção para cima, temos:
Passo 3
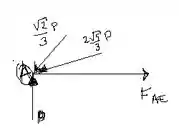
Vamos agora fazer a análise de forças na junta . O somatório das forças nos eixos de referência (, para um corpo em equilíbrio, deve ser igual a zero.

Assim, adotando como referências positivas as direções para direita e para cima, temos:
Passo 4
Vamos agora analisar o ponto . O somatório das forças nos eixos de referência (, para um corpo em equilíbrio, deve ser igual a zero. Porém, antes de escrever a soma das forças, precisamos descobrir o seno e cossenos dos ângulos dessa treliça para que possamos decompor as forças, beleza?
Olhando o triângulo ACF, temos:
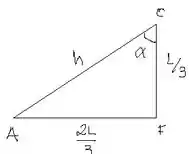
Aplicando o teorema de Pitágoras, temos:
Assim, o cosseno de é igual a: e o seno igual a: .
Agora olhando o triângulo :
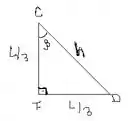
Aplicando o teorema de Pitágoras, temos:
Assim, o cosseno de é igual a: e o seno igual a:
Por ultimo, vamos olhar pro triângulo :

Aplicando o teorema de Pitágoras, temos:
Assim, o cosseno de é igual a: e o seno igual a:
Passo 5
Adotando como referências positivas as direções para direita e para cima, temos:
Passo 6
Vamos agora analisar o ponto . As duas treliças são iguais, o que nos leva a ter os mesmos valores para os ângulos e tamanhos dos braços.
O somatório das forças nos eixos de referência (, para um corpo em equilíbrio, deve ser igual a zero. Adotando como referência positiva a direção para direita, temos:
Passo 7
Como , podemos achar o valor de Usando a equação que encontramos ao final do passo , temos: