Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Mecânica para Engenharia Estática - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 6.Problemas - Ex. 26

6.26. Um painel está sujeito a uma carga de vento que exerce forças horizontais de 1,5   k N nos nós B e C de uma das treliças de apoio laterais. Determine a força em cada membro da treliça e indique se os membros estão sob tração ou compressão.

Passo 1

Vamos usar a lei dos nós para resolver este exercício. Começando de cima para baixo, temos o ponto C, então

F R x = 0

F R x = 1,5 - F C D ⋅ sin ⁡ θ = 0

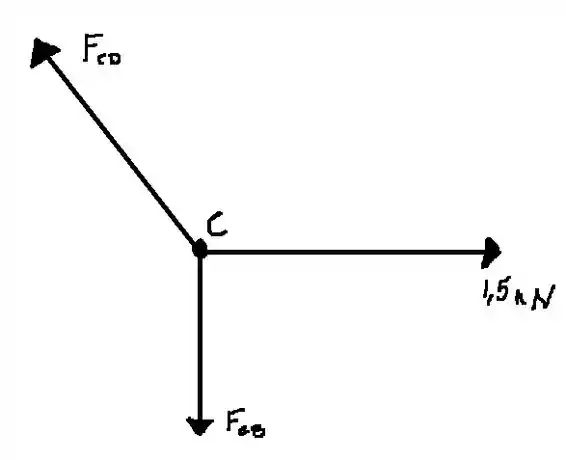
Nós podemos determinar θ através do triângulo formado pela figura

θ = t a n - 1 1,5 3,6 = 22,62 °

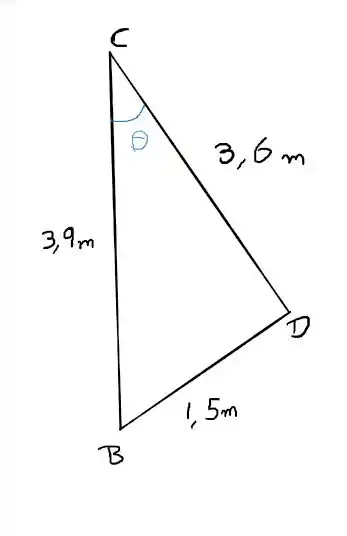
Então

F C D = 1,5 sin ⁡ 22,62 ° = 3,9   k N

F C D tem uma força de contração, pois ela é direcionada à C

Agora faremos para o eixo y

F R y = 0

F R y = - F C B + F C D ⋅ cos ⁡ θ = 0

Então

F C B = F C D ⋅ cos ⁡ θ = 3,9 ⋅ cos ⁡ 22,62 ° = 3,6   k N

F C B tem uma força de tração, pois ela é contrária à C

Passo 2

Agora vamos fazer a análise para o ponto D.

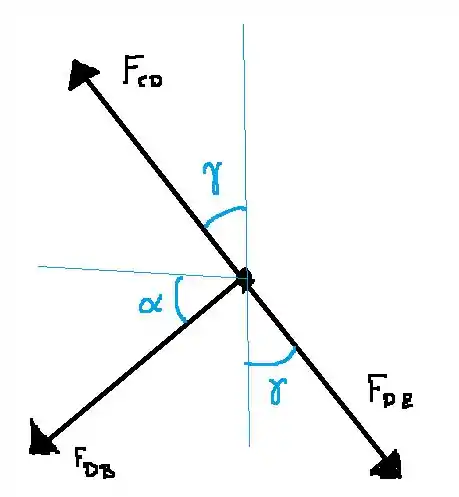
Seguindo o mesmo raciocínio que fizemos para o passo anterior, temos

F R x = 0

F R x = - F D B ⋅ cos ⁡ α = 0

Pela imagem vemos que cos ⁡ α ≠ 0   então

F B D = 0

Agora faremos para o eixo y

F R y = 0

F R y = F C D ⋅ cos ⁡ γ - F D E ⋅ cos ⁡ γ = 0

Então

F D E = F C D = 3,9   k N

F D E tem uma força de contração, pois ela é direcionada à D

Passo 3

Agora faremos o mesmo para o ponto B

F R x = 0

F R x = 1,5 - F B A ⋅ cos ⁡ 45 ° + F B E ⋅ sin ⁡ ϕ = 0

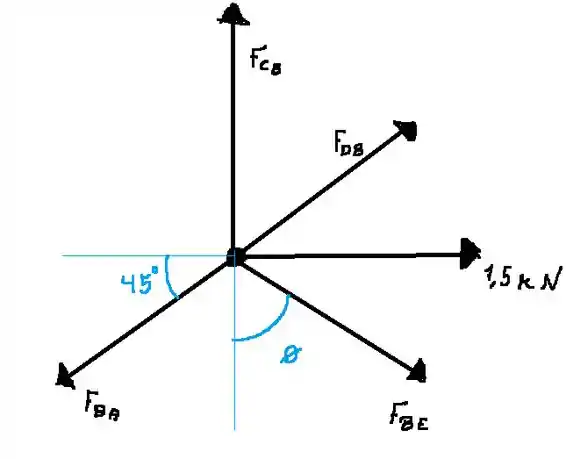
Nós podemos determinar ϕ através do triângulo formado pela figura

ϕ = 180 ° - 2 ⋅ α = 180 ° - 2 ⋅ t a n - 1 3,6 1,5 = 45,24 °

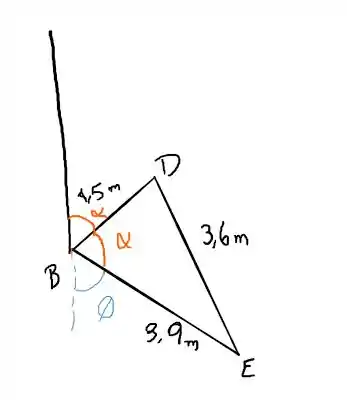
Então

1,5 - F B A ⋅ cos ⁡ 45 ° + F B E ⋅ sin ⁡ 45,24 ° = 0

Agora faremos para o eixo y

F R y = 0

F R y = F C B - F B A ⋅ sin ⁡ 45 ° - F B E ⋅ cos ⁡ ϕ = 0

Então

3,6 - F B A ⋅ sin ⁡ 45 ° + F B E ⋅ sin ⁡ 45,24 ° = 0

Agora temos duas equações

1,5 - F B A ⋅ cos ⁡ 45 ° + F B E ⋅ sin ⁡ 45,24 ° = 0     1

3,6 - F B A ⋅ sin ⁡ 45 ° - F B E ⋅ cos ⁡ 45,24 ° = 0     ( 2 )

E duas incógnitas F B A   e   F B E

Isolando F B E em (1)

F B E = - 1,5 + F B A ⋅ cos ⁡ 45 ° sin ⁡ 45,24 °    

Substituindo em (2)

3,6 - F B A ⋅ sin ⁡ 45 ° - - 1,5 + F B A ⋅ cos ⁡ 45 ° sin ⁡ 45,24 °     ⋅ cos ⁡ 45,24 ° = 0    

3,6 - F B A ⋅ sin ⁡ 45 ° + 1,5 ⋅ tan ⁡ 45,24 ° - F B A ⋅ cos ⁡ 45 °   ⋅ tan ⁡ 45,24 ° = 0    

Então

F B A - sin ⁡ 45 ° - cos ⁡ 45 ° ⋅ tan ⁡ 45,24 ° = - 1,5 ⋅ tan ⁡ 45,24 ° - 3,6

F B A = - 1,5 ⋅ tan ⁡ 45,24 ° - 3,6 - sin ⁡ 45 ° - cos ⁡ 45 ° ⋅ tan ⁡ 45,24 ° = 3,6   k N

F B A tem uma força de tração, pois ela é contraria à B

Logo

F B E = - 1,5 + 3,6 ⋅ cos ⁡ 45 ° sin ⁡ 45,24 ° = 1,47   k N  

F B E tem uma força de tração, pois ela é contraria à B

Resposta

F C D = 3,9   k N   ( C )

F C B = 3,6   k N   ( T )

F B D = 0

F D E = 3,9   k N   ( C )

F B A = 3,6   k N   ( T )

F B E = 1,47   k N     ( T )

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Determine a força desenvolvida em cada membro da treliça espacial e indique se os membros estão sob tração ou compressão. A caixa possui um peso de 750N .
Determine a força nos membros F E e E D da treliça espacial e indique se os membros estão sob tração ou compressão. A treliça é sustentada por juntas esféricas em C e ligações curtas em A e B .
Determine a força nos membros B E , D F e B C da treliça espacial e indique se os membros estão sob tração ou compressão.
Determine a força nos membros A B , A E , B C , B F , B D e B E da treliça de espaço e indique se os membros estão sob tração ou compressão.
Determine a força nos membros A B , C D , E D e C F da treliça espacial e indique se os membros estão sob tração ou compressão.