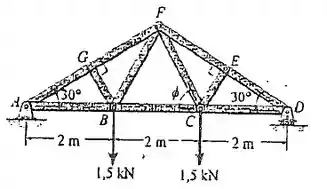
Determine a força nos membros da treliça. Diga se os membros estão sob tração ou compressão.
Passo 1
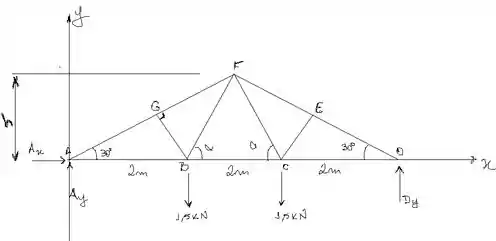
Vamos desenhar o diagrama de corpo livre dessa treliça!
Passo 2
Se traçarmos uma seção pelos membros e e analisar a porção da treliça à direita, iremos perceber que existem quatro forças atuando com valores desconhecidos ( e . Portanto, devemos determinar primeiro a força de reação no ponto a partir do diagrama livre de forças.
A altura da treliça é dada por:
Então, os membros diagonais fazem um ângulo com a horiontal igual a:
Passo 3
Para um corpo em equilíbrio, o somatório dos momentos em relação em um ponto é igual a zero. Assim, calculando o momento em relação ao ponto e adotando como sentido positivo o horário, temos:
Passo 4
Agora que determinamos nós podemos traçar a seção pelo membros e analisar a porção da treliça à direita. Vamos aqui assumir que os membros que não conhecemos estão sendo tracionados.
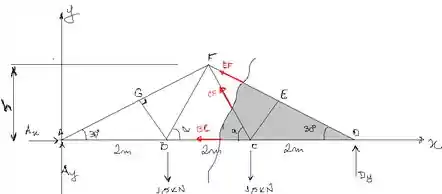
Analisando o somatório dos momentos em relação ao ponto , eliminamos as forças por estarem na mesma linha de ação do ponto.
Passo 5
O somatório das forças nos eixos de referência (, para um corpo em equilíbrio, deve ser igual a zero. O somatório das forças nos eixos de referência (, para um corpo em equilíbrio, deve ser igual a zero. Adotando como referência positiva as direções para direita e para cima, temos:
Agora para o eixo :
Resposta
As forças são: