Enunciado
Mecânica e Resistência dos Materiais - Beer - Mecânica dos Materiais- Ed: 7º - Capítulo 10.Problemas - Ex. 7
10.7 A barra rígida AD está conectada a duas molas de constante k e está em equilíbrio na posição indicada. Sabendo que as cargas iguais e opostas P e P’ permanecem horizontais, determine a intensidade da carga crítica para o sistema.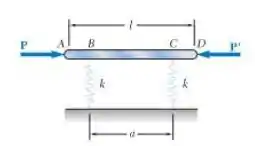 
Passo 1
Galerinha, vamos ver os dados que temos para usarmos as fórmulas e realizar nosso cálculo:
Sejam as deflexões dos pontos B e C, positivas para cima.
Passo 2
Seja a mudança de ângulo.
P e P’ formam um par de magnitude P no sentido horário.
Resposta
Então gurizada, como acabamos de calcular, temos a resposta de
Exercícios de Livros Relacionados
Uma coluna de aço biarticulada, de 100x100m de seção transversal é apoiada como mostrado no Prob. 11.25. Sabendo-se que inicialmente a força na coluna é zero, determinar o comprimento L necessário, se
Uma coluna de comprimento efetivo L pode ser confeccionada pregando-se firmemente as pranchas idênticas, tal como mostrado. Para a espessura das pranchas indicadas, determinar a razão entre a carga cr
O projeto de uma barra vazada de aço requer uma área da seção transversal de 1000mm². Sabendo-se que o comprimento efetivo da barra é de 2m, determinar a carga crítica quando a razão entre o diâmetro
Uma coluna de 2,5m de comprimento efetivo é feita da metade de um perfil laminado de aço W200x52. Usando-se as propriedades geométrica da seção transversal mostrada, determinar o coeficiente de segura
Duas barras de latão usadas como membros em compressão, cada uma delas com 1,8m de comprimento efetivo, tem as seções transversais mostradas. Determinar. (a) a espessura da parede da barra vazada quad